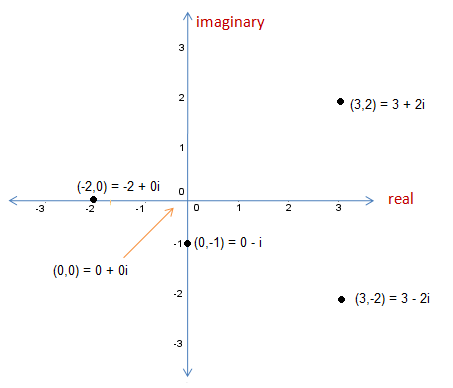
Closure Property and Imaginary Numbers
If an operation is performed on any two numbers in a set and the result is still in that set, we say that the set is closed under that operation. For example, we can say that the set of positive integers is closed under addition because if we add any two positive integers, the result is still a positive integer. On the other hand, the set of positive integers is NOT closed under subtraction because in many cases, the result is a negative integer (e.g 9 – 12 = -3). The video below is one of the best videos I’ve seen so far explaining closure property This video is just one of a series of videos about Imaginary Numbers.
Did you enjoy the video? If yes, kindly share it to your friends.