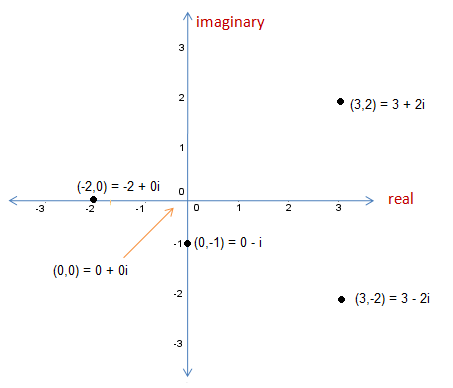
Introduction to the Complex Plane
Imaginary numbers had no use when it was invented except for intellectual exploration until it was linked to coordinate geometry. The complex number can be plotted as the ordered pair
where
is the real part and
is the imaginary part. Therefore, the complex numbers
,
,
, and
can be plotted as
,
,
, and
in a “coordinate plane” respectively as shown below. In the figure, we can see that the origin is
and that
, the complex conjugate of
, is its reflection along the x-axis (Can this be generalized?).
The plane where the complex numbers are plotted above is called the complex plane.
In the complex plane, we can observe that all numbers of the form are real numbers and these numbers are represented by the horizontal axis. The numbers of the form
are all imaginary numbers and it is represented by the vertical axis. Thus, we can call them the real axis and the imaginary axis respectively.
In addition, we can conclude that all real numbers are complex numbers since for all real numbers ,
. So, the set of real numbers is a subset of the set of complex numbers.