Triangular Numbers and the Sum of the First n Positive Integers
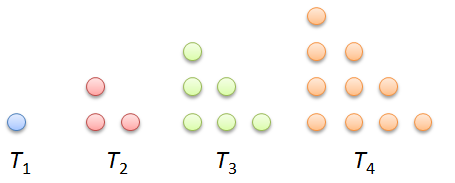
The numbers 1, 3, 6, 10, 15, … are called triangular numbers because they could be arranged in the form of triangles. Triangular numbers is one of the polygonal numbers — numbers that can represented by dots to form regular polygons.
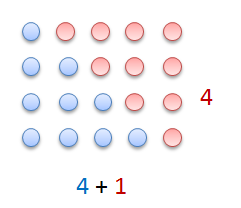
Finding the nth triangular number is quite easy. All we have to do is form a rectangle using the “dot representation” of two triangular numbers. For example, we want to find the fourth triangular number, we create dots representing two triangular numbers, and then use them to form a rectangle. The area of the formed rectangle is .
Since the triangle is half the rectangle, the fourth triangular number is which is equal to 10. Clearly, this method can be generalized. To find the nth triangular number, we create dots representing two triangular numbers with side length n. We use them to form a rectangle with area
. We divide the area by 2 giving us
,
the nth triangular number.
From the first figure, we observe the following:
Generalizing the pattern above, we have
.
Notice that calculating for is the same as finding the sum of the first
positive integers, which we have already discussed to be
.
Triangular numbers and other polygonal numbers were explored since the ancient times, particularly by the Pythagoreans. The Pythagoreans believed that everything in the universe can be represented by numbers. They also believed that variety of shapes can be described by the arrangements of their particles.