Another Proof of the Sum of the First n Positive Integers
We have discussed how Gauss was able to devise a clever way to add the first positive integers at a very young age in a few minutes. We generalized his method and have also seen the link between the sum and the area of a triangle. In both discussions, we have shown that the sum of the first
positive integers is
.
In this post, we discuss another geometric proof of the problem above. We start with a specific case adding the first positive integers, and the proceed to the general case.
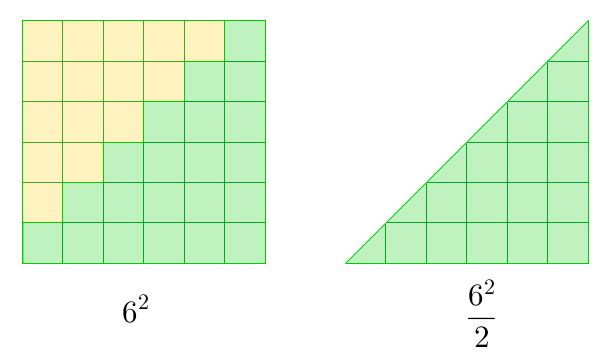
We can add the first positive integers manually or just by counting the number of unit squares in the figure above. The figure shows the geometric representation of the sum of the first 6 positive integers. Adding manually is not difficult if the given is small. However, we need a strategy for larger numbers.
One strategy is to “complete the largest square” by adding unit squares. In the given above, we can add unit squares (see yellow squares below) so that it forms a square. If we divide the square diagonally and remove half of it, the remaining number of squares is
.
However, half squares from the original figure were also removed when we performed the division. Therefore, we have to return
squares. So, the total number of squares is
.
Now, suppose we want to find the sum of all positive integers from to
, then we create a
unit squares. We then divide it half diagonally and remove half of it leaving
unit squares left. We then return
squares. So, the total number of squares, or the sum of the first
positive integers is
.
In general, if we want to find the sum of the first positive integers, we have create an
unit squares. We divide it diagonally and leave
unit squares. We then return
squares. So the sum of all the numbers from
to
, or equivalently, the total number of squares, is equal to
.