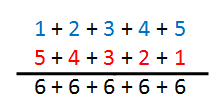Linking sum of counting numbers to triangle area

We have discussed how Gauss was able to add the first 100 counting numbers, and we learned ways how to generalize his method.  In this post, we link his method in finding the area of triangles.

Adding the first few counting numbers is easy. However, as the numbers become larger, it becomes harder. According to an anecdote, Gauss at primary school was able to find a clever way of answering the question his teacher asked him:  What is the sum of all the numbers from 1 to 100?

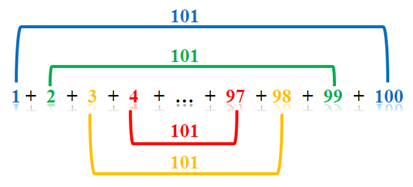Gauss method was to add the first and the last digit (1 and 100), the second and the second to the last digit (2 and 99), third and the third to the last digit (3 and 98), and found out that the sums were always 101. There are 50 pairs of numbers from 1 to 100 whose sum is 101. So,  the sum of all the numbers from 1 to 100 is (101)(50) = 5050.

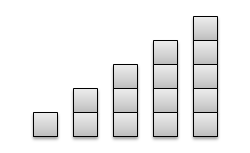
Finding the sum of the first n counting numbers may also be represented as stacked squares as shown in the next figure. Counting the squares in the first diagram is the same as adding the first 5 natural numbers: 1 + 2 + 3 + 4 + 5 = 15.

 

Similar to Gauss’ method is adding the numbers: the first addend in increasing order, and the second in decreasing order as shown in the third figure. Let us note, though, that the numbers are added twice here; therefore, the sum must be divided by 2.

The geometric representation of the preceding addition is shown in the next figure. The ‘blue numbers’ are represented by the blue squares and the ‘red numbers’ are represented by the red squares. All the squares add up to 6: 1 goes to 5, 2 goes to 4, 3 goes to 3, and so on. The sum of the two numbers is represented by the 5 by 6 rectangle. Since we have counted the number twice, we divide them by 2, making it 15.

Let us look the geometric interpretation of this method. Adding the first 5 integers is having 5 rectangles where in each rectangle is composed of 6 squares. This is similar to finding the area of a rectangle with length base 5 units and height 6 units. And, dividing it by 2 is the same as finding the area of a right triangle, again, with base 5 units and height 6 units.

In general, the representation above can be used to derive the area of a right triangle. Given a base and the height, how do we compute the area? Well — we create another triangle congruent to it, form a rectangle using them, find the area of the rectangle formed, and then divide the area by 2.

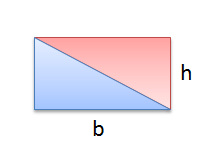Therefore, the area of a right triangle is the product of its base and height divided by 2.