Tag: sum of first n natural numbers

Another Proof of the Sum of the First n Positive Integers

High School Mathematics, High School Number Theory

We have discussed how Gauss was able to devise  a clever way to add the first 100 positive integers at a very young age in a few minutes. We generalized his method and have also seen the link between the sum and the area of a triangle. In both discussions, we have shown that the sum of the first n positive integers is \frac{n(n+1)}{2}.

In this post, we discuss another geometric proof of the problem above.  We start with a specific case adding the first 6 positive integers, and the proceed to the general case.

We can add the first 6 positive integers manually or just by counting the number of unit squares in the figure above. The figure shows the geometric representation of the sum of the first 6 positive integers. Adding manually is not difficult if the given is small. However, we need a strategy for larger numbers. » Read more

4 comments , , ,

Linking sum of counting numbers to triangle area

High School Algebra, High School Geometry, High School Mathematics

We have discussed how Gauss was able to add the first 100 counting numbers, and we learned ways how to generalize his method.  In this post, we link his method in finding the area of triangles.

Adding the first few counting numbers is easy. However, as the numbers become larger, it becomes harder. According to an anecdote, Gauss at primary school was able to find a clever way of answering the question his teacher asked him:  What is the sum of all the numbers from 1 to 100?

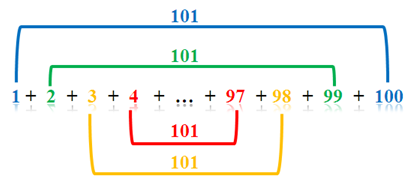Gauss method was to add the first and the last digit (1 and 100), the second and the second to the last digit (2 and 99), third and the third to the last digit (3 and 98), and found out that the sums were always 101. There are 50 pairs of numbers from 1 to 100 whose sum is 101. So,  the sum of all the numbers from 1 to 100 is (101)(50) = 5050. » Read more

One comment , , ,