Tag: polygonal numbers

Triangular Numbers and the Sum of the First n Positive Integers

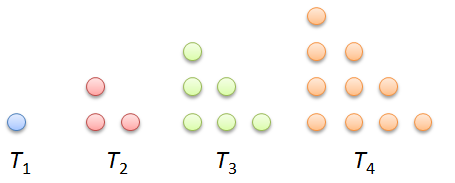
High School Mathematics, High School Number Theory

The numbers 1, 3, 6, 10, 15, … are called triangular numbers because they could be arranged in the form of triangles. Triangular numbers is one of the polygonal numbers — numbers that can represented by dots to form regular polygons.

Finding the nth triangular number is quite easy. All we have to do is form a rectangle using the “dot representation” of two triangular numbers. For example, we want to find the fourth triangular number, we create dots representing two triangular numbers, and then use them to form a rectangle. The area of the formed rectangle is 4(4+1). » Read more

2 comments , , ,

Generating Pythagorean Triples from Square Numbers

College Mathematics, High School Mathematics, Number Theory

A figurate number is a number that can be represented by a regular geometrical arrangement of equally spaced points (or circles as shown in the first figure). If the arrangement forms a regular polygon, the number is called a polygonal number.

Examples of polygonal numbers are square numbers. The first  four square numbers are 1, 4, 9, and 16, and their geometric representations are shown in the first figure. It is clear that that the 10th square number has 102 circles, and in general, the nth square number has n2 circles.

Looking at the color pattern above, we can see that there is something very special about square numbers. Each square number can be represented as the sum of odd integers.  The first four examples are shown below. » Read more

3 comments , , , ,