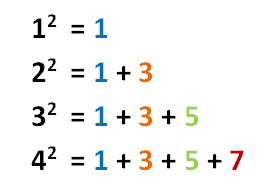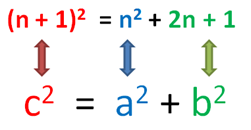Generating Pythagorean Triples from Square Numbers
A figurate number is a number that can be represented by a regular geometrical arrangement of equally spaced points (or circles as shown in the first figure). If the arrangement forms a regular polygon, the number is called a polygonal number.
Examples of polygonal numbers are square numbers. The first four square numbers are 1, 4, 9, and 16, and their geometric representations are shown in the first figure. It is clear that that the 10th square number has 102 circles, and in general, the nth square number has n2 circles.
Looking at the color pattern above, we can see that there is something very special about square numbers. Each square number can be represented as the sum of odd integers. The first four examples are shown below.
From the pattern above, we can see that 22 is the sum of the first 2 positive odd integers, 32 is the sum of the first 3 odd integers, and so on. In general, we can say that the n2 is the sum of the first n positive odd integers. This is actually true and can easily be proven using mathematical induction. The proof is left as an exercise.
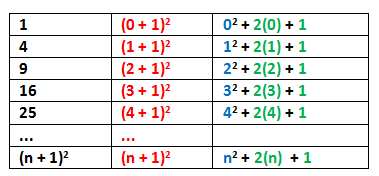
Looking at the table below, we can make numerical expressions to represent square numbers. Generalizing these numerical expressions, we see that the following equation holds:
.
Note that if is a perfect square, the three numbers will satisfy the Pythagorean Theorem, and since
is an integer, it follows that
are Pythagorean Triples.
Now, assuming that is a square number, then
for some positive integer
. Solving for
, we have
. Since we want
to be a positive integer,
must be positive odd integers greater than 1 (Why?). This implies that for all odd positive integers
,
is a Pythagorean Triple.
For example, , then
. This gives us the triple
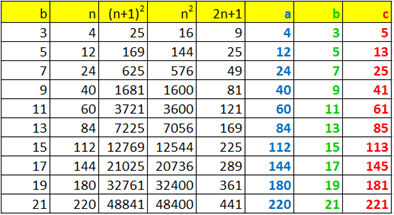
. The first ten values of
and the corresponding Pythogorean Triples are shown in the table below.
From the table, it is clear that we can generate infinitely many Pythagorean Triples using the method above.