Curve Sketching 4: Identifying Oblique Asymptotes
In the previous post in this series, we have learned about asymptotes. horizontal asymptote and vertical asymptote. We continue this series by discussing oblique asymptotes in this post.
An oblique asymptote is an asymptote that is not vertical and not horizontal. We need to know these types of asymptotes to sketch graphs especially rational functions. A rational function contains an oblique asymptote if the degree of its numerator is 1 more than that of its denominator. For instance, the function
has degree 2 in the numerator and 1 in the denominator. If we divide the expression, we have
.
Notice that as goes to infinity, the remainder goes to 0. The expression
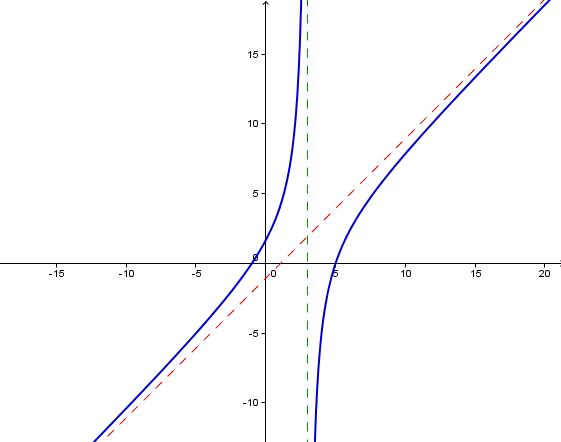
is the oblique asymptote.
The red dashed line in the graph is the oblique asymptote of the function above. Notice that the function has also a vertical asymptote (see green dashed line) which is .
Note however, that if the degree of the numerator of the rational function is more than the degree of the denominator, but not 1, there are no oblique asymptotes. In addition, there is at most one oblique asymptote or one horizontal asymptote, but not both (Why?).
Reference: Bob Miller’s Calc for the Clueless: Calc I