Curve Sketching 3: Vertical and Horizontal Asymptotes

Curve Sketching 3: Understanding Vertical and Horizontal Asymptotes

This is the third part of the Mathematics and Multimedia Curve Sketching Series. In the first part of this series, we have learned how to sketch linear functions, while in the second part, we have learned how to sketch quadratic functions. In this post and the next post, we will discuss about another important property of some functions that can be used in curve sketching.

In Curve Sketching 2, we have learned the different properties of quadratic functions that can help in sketching its graphs. This property is called the asymptote.

An asymptote is a line that the curve gets very very close to but never intersect. There are three types of asymptotes: vertical, horizontal, and oblique. In this post, we discuss the vertical and horizontal asymptotes.

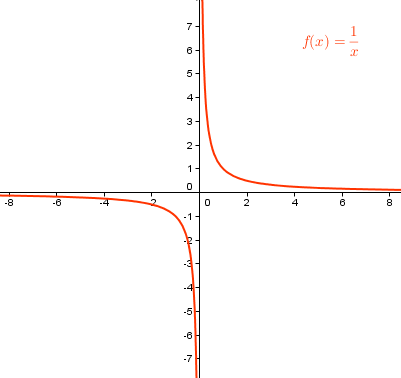
In the graph above, the vertical and the horizontal asymptotes are the y and x axes respectively. In the remaining part of this post, we will use mostly rational functions to illustrate asymptotes.

Vertical Asymptote

The rational function $f(x) = \frac{1}{x}$ above has a vertical asymptote . As x gets closer to 0 (try moving the mouse pointer from right to center or from left to center along the x-axis and observe the value of $f(x)$ ), $f(x)$ either goes very large or very small (negative). From the example above, clearly, anything that makes the denominator of the rational function close 0 is its vertical asymptote. Also, some functions have more than one asymtpotes such as the one show below.

Exercise: Using a graphing calculator or a graphing software, graph

$g(x) = \displaystyle\frac{x - 4}{(x-1)(x+2)}$

has vertical asymptotes $x = 1$ and $x = -2$ .

Horizontal Asymptote

Note to Students: The study of horizontal asymptote is easier if you have already discussed limits.

If $P(x)$ and $Q(x)$ are polynomial functions, the rational function $h(x) = \frac{P(x)}{Q(x)}$ has horizontal asymptote $y=0$ if the the degree of $P$ is less than the degree of $Q$ . For example, the rational function

$h(x) = \displaystyle\frac{x^2-1}{3x^5 - 2x}$

will approach to $0$ as $x$ becomes larger and larger. In limits,

$\lim_{x \to \infty} \displaystyle\frac{x^2-1}{3x^5 - 2x} = 0$ .

If the degree of $P$ and $Q$ are equal, this will leave all terms $0$ as $x$ becomes larger and larger. The term that will be left are those with the highest degree. For instance,

$h(x) = \displaystyle\frac{4x^3 - 3x^2 + 8}{-5x^3 - 3}$

has a horizontal asymptote

$y = -\displaystyle\frac{4}{5}$

since

$\lim_{x \to \infty} \displaystyle\frac{4x^3-3x^2+8}{-5x^3-3} = -\displaystyle \frac{4}{5}$ .

These types of asymptotes will help us more determine the appearance of the graph of the function that we are trying to sketch. In the next post, we will discuss oblique asymptotes.

By the way, a more detailed explanation about asymptote can be found in Mathematics Concepts Explained.

3 comments on “Curve Sketching 3: Understanding Vertical and Horizontal Asymptotes”

Pingback: Curve Sketching 4: Oblique Asymptotes

Shaun on March 5, 2013 at 1:34 pm said:

Hi Guillermo,

Somehow I missed this article when you posted it. I really like it! I put up a post not too long ago on my site that explains asymptotes as well, but yours is much more concise. I have actually gone back to that post and inserted a link to this article of yours. I thought it might be nice to provide a second perspective and different examples to help explain the concept.

Shaun

Reply ↓

Guillermo Bautista on March 5, 2013 at 3:22 pm said:

Thank you very much Shaun. I read your post and it is also very informative that I had linked it to mine.

Reply ↓