10 Math Problems That Look Easy But Immensely Difficult to Solve
There are thousands of math problems that are difficult for a common person to understand even though mathematicians may find them easy to solve. On the other hand, there are math problems that look really easy that even a middle student would understand the way they are stated, but their solution or proof is immensely difficult. Yes, such math problems exist and below are the some of the most well known.
1. Squaring the Circle
Squaring the circle is one of the classic math problems proposed by Geometers.
It was a challenge to use compass and straightedge to construct a square with the same area as a given circle in a finite number of steps. Although the circle to square approximation was known since the time of the ancient Babylonian mathematicians, it was Anaxagoras (c. 510 – 428 BC) who was the first to be recorded in history to work on the problem.
In 1882, Ferdinand von Lindemann proved that was transcendental. The consequence of this is the impossibility of squaring the circle.
2. Twin Prime Conjecture
Prime numbers are positive integers that are divisible only by and itself. The first 10 prime numbers are
, and
. Twin Primes are pair of primes with difference
. The pairs
,
,
and
are twin primes. The greatest twin primes as of this writing are
and
both primes consisting digits (reference). Now the question is how many twin primes are there?
Although the infinitude of primes was proved as early as the time of Euclid, the Twin Prime Conjecture is still one of the most elusive math problems until now. Although mathematicians believe that the conjecture is true, the answer still remains a mystery.
3. Goldbach’s Conjecture (2 conjectures)
This math problem was proposed by German mathematician Christian Goldbach to Leonhard Euler in 1742 and is still unsolved until now. It states that every even integer greater than can be expressed as a sum of two primes. The following are examples:
,
,
, and
. The image below shows that this is true up to
.
In fact, as of this writing, it has been tested to be true up to but is still unproven in general.
Another version of this math problem also exists, the Goldbach’s weak conjecture. It states that every positive integer greater than can be expressed as sum of three primes given that a prime may be used more than once in the same sum
4. Fermat’s Last Theorem
Everybody who has taken high school mathematics is familiar with the Pythagorean Theorem. This theorem has hundreds of proofs. The Pythagorean Triples where
are lengths of right triangles and satisfy the Pythagorean Theorem equation
.
Although we can find infinitely many triples (e.g. mulitply by any positive integer) that satisfy the Pythagorean Theorem, the Fermat’s Last Theorem states that there are no positive integers
. that satisfy the equation with higher degree than
. That is, for every triple
, the following inequalities are always true.
.
In general, it says that there is are no positive integers ,
,
that satisfy the equation
, for any integer
greater than
.
This math problem was proposed by Pierre de Fermat in 1637, and after more than 300 years and the many incorrect proofs published, Andrew Wiles finally solved the enigma in 1995. It took him 8 years to solve the problem!
5. Catalan’s Conjecture
The Catalan’s conjecture states that only and
are the powers of two natural numbers whose values 8 and 9 are consecutive. This was conjectured by an Eugène Charles Catalan in 1844 and proven in 2002 by Preda Mihăilescu.This means that aside from the pair above, there is no solution to the equation
where 1.
6. Four Color Theorem
The Four Color Theorem states that given a “map” with contiguous regions, the minimum number of colors that you can place where no adjacent of the same color is 4.
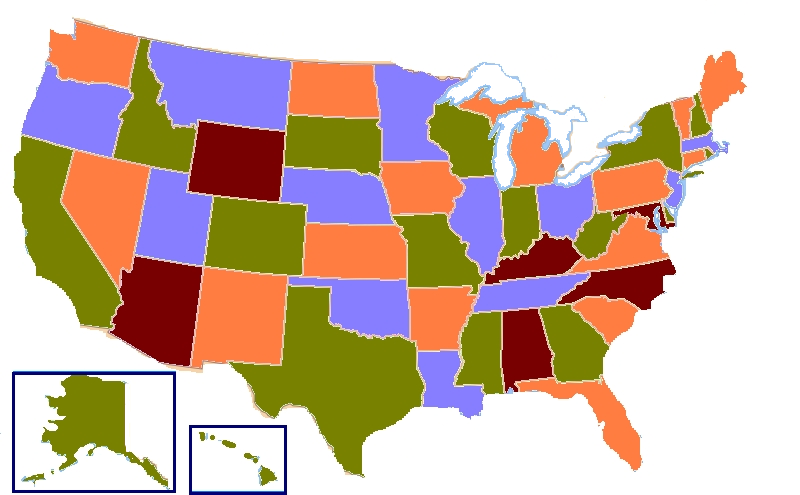
It was proposed by Francis Guthrie in 1852 and was proved by Kenneth Appel and Wolfgang Haken in 1976. It was the first major theorem to be proved using a computer.
7. Collatz Conjecture
Take any natural number. If even, divided by . If odd, multiply by
and add
. The Collatz conjecture states that no matter what number you choose at first, doing this repeatedly will eventually result to 1. The conjectures is still unsolved to this day.
8. Perfect Number Conjectures (2 conjectures)
A perfect number is a positive integer that is equal to the sum of its proper divisors (the divisors less than it). The smallest perfect numbers is : its divisors are
,
, and
and
. The next perfect number is
(
. Perfect numbers are very rare. As of this writing, there are only
known perfect numbers, and no one knows if there are infinitely many of them. All known perfect numbers are also even and no one also knows if an odd perfect number exists.
The problems above show one aspect of mathematical beauty. That sometimes, the simple math problems (to state) are the most difficult to solve.