High School Algebra Archives - Page 23 of 31

Folding a Hyperbola

April 28, 2011 GB High School Algebra, High School Mathematics

Below is an activity that uses paper folding to create a parabola. The steps are as follows.

First, draw a circle on a piece of paper and draw a point outside the circle. Second, draw a point on any location on the circumference of the circle. Third, fold the paper such that the point on the circle and the point outside the circle are coinciding, and then make a crease.

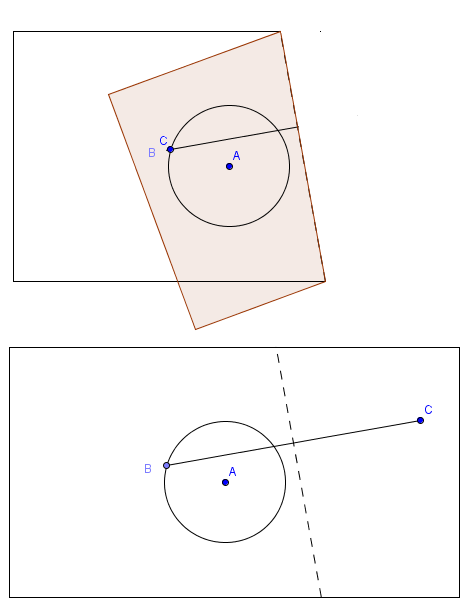Fourth, repeat the second and third steps over and over again.

The border of the creases made on the paper will form a hyperbola. The more number of folds, the more apparent the hyperbola.

The construction above is simulated in the Folding a Hyperbola applet at GeoGebra Applet Central.

Military drills and the closure property of real numbers

In military drills, we are familiar with the commands that let the soldiers face or turn to certain directions. Left face (sometimes called left turn), right face, and about face are probably the most common commands used. If we are facing north, a left face would mean turning left 90 degrees, which means facing west. In the following discussion, we will agree that our starting position is facing north. We will call this position, the standard position.

Let us represent the turns with letters:A for about face, R for right face, and L for left face. Notice that whatever combination of turns we do, L, R or A, the result is confined to the four directions. An R followed by an A is equivalent to an L (facing west) with respect to the standard position. Likewise an L followed by another L is equivalent to A.We will to denote our starting position P as reference; it is not turn command, so if the soldier is not facing north (see second figure), a P will just mean that the soldiers remain in their current position. » Read more

5 comments closure property, closure property of natural numbers under addition, closure property of natural numbers under division, closure property of natural numbers under multiplication, closure property of natural numbers under subtraction, natural numbers, non-negative numbers

The Commutativity of Real Numbers

March 10, 2011 GB High School Algebra, High School Mathematics

In the previous discussion, we have shown that addition of two integers a and b is commutative by considering a and b as lengths of two segments. Joining the two segments is the same as adding two integers. We have observed that a + b equals b + a.

We have also shown that multiplication of two integers a and b is commutative by considering a and b as side lengths of a rectangle. Getting the area of a rectangle with side lengths a and b is the same as multiplying a and b. We have observed that ab equals ba. However, we argued about commutativity that any segment does not change its length and the movement of rectangles does not change its area. This reasoning is only limited to positive integers because we cannot represent negative integers as length or area. To explore further, we use the addition and multiplication tables to see if the addition and multiplication of integers are both commutative.

« 1 … 21 22 23 24 25 … 31 »