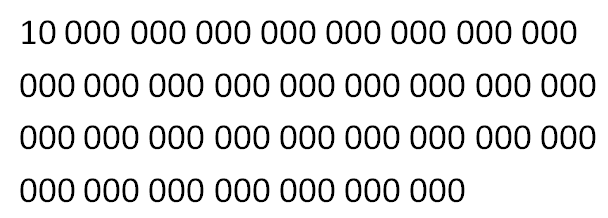What If We Have 12 Fingers?
Our number system is called the decimal system (deci means 10) because we count in groups of 10’s. This is probably because we have 10 fingers. What do I mean when I said when we count in groups of 10?

Our number system has the digits 0 to 9, and then we when we reach the 10th number, we place 1 in the tens place 0 in the ones digit. In the decimal number system, 23 means that we have 2 tens and 3 ones. Similarly, the number 452 means that we have 4 groups hundreds (10 tens), 5 groups of tens and 8 ones. In fact, if we use the expanded notation, 452 is equal to
.
Notice that each number is multiplied by powers of 10. » Read more