binomial theorem Archives - Math and Multimedia

The Binomial Expansion

July 5, 2010 GB College Mathematics, Combinatorics, High School Mathematics

Note: This is the second part of the Binomial Expansion Series

Part I: Milkshakes, Beads, and Pascal’s Triangle

Part II: Binomial Expansion

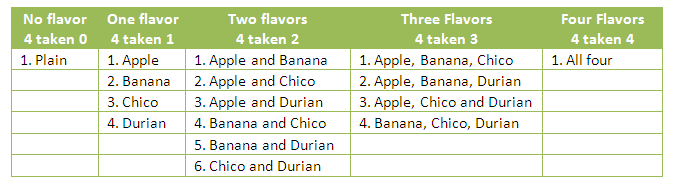
In the Milkshakes, Beads, and Pascal’s Triangle article, we have shown that the combination of the binary numbers 1 and 0 may be interpreted as the number the flavors of milk shakes, or the number of possible paths of the bead in our Galton board as shown in Table 1. Recall that in the Milkshake problem, Issa was given a choice to combine any number of flavors from four fruits: Apple, Banana, Chico and Durian. Thus, 0101 means banana-durian milkshake. On the other hand, in the beads problem, 0101 is LRLR or the bead went to the left after hitting the peg in row A, right in after hitting the peg in row B, left after hitting the peg in row C and right after hitting the peg in row D. » Read more

One comment binomial expansion, binomial expansion help, binomial theorem, Galton board, n objects taken k at a time, pascal's triangle, permutations and combinations

Milkshakes, Beads, and Pascal’s Triangle

June 28, 2010 GB College Mathematics, Combinatorics, High School Mathematics

Note: This is the first part of the Binomial Theorem Series

Binomial Theorem I: Milkshakes, Beads, and Pascal’s Triangle

Binomial Theorem II: The Binomial Expansion

*************************************

The Milk Shake Problem

Problem 1: Issa went to a shake kiosk and want to buy a milkshake. The shake vendor told her that she can choose plain milk, or she can choose to combine any number of flavors in any way she want. There are four flavors to choose from: Apple, Banana, Chico, and Durian.

How many possible combinations can Issa create?

It is clear that Issa can choose her milk shake to have no flavor (pure milk shake), one flavor, two flavors, three flavors, or four flavors. The possible combinations are shown below.

Table 1