Divisibility by 3
This is post is the fourth part of the Divisibility Rules Series. The first three posts are about divisibility by 2, divisibility by 4 and divisibility by 5 and 10. In this post, we discuss divisibility by 3.
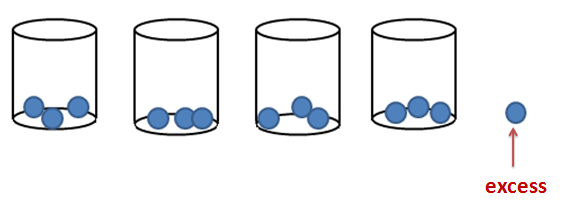
When we divide things, we split them into ‘groups.’ Of course, we cannot always divide them equally. For example, dividing 13 balls by 3 is the same as putting the balls into containers in groups of three. In dividing 13 by 3, 1 is left out as shown below. We have learned that the excess or the ones that are left out during division are called remainders. In the figure below, we can say that 13 divided by 3 gives a remainder of 1.
Divisibility by 3 is not as easy as divisibility by 2, by 5 or by 10. However, we note the following observations when we divide by 3. » Read more