Sum of the interior angles of a polygon
We were taught that if we let be the angle sum (the total measure of the interior angles) and
be the number of vertices (corners) of a polygon, then
. For example, a quadrilateral has
vertices, so its angle sum is
degrees. Similarly, the angle sum of a hexagon (a polygon with
sides) is
degrees.
But where did this formula come from? Does this formula work for all polygons? (Note that in this discussion, when we say polygon, we only refer to convex polygons).
Before we answer these questions, let us first have a brief review of some elementary concepts.
Polygons and Interior Angles
A polygon is a closed figure with finite number of sides. In the figures below, is a polygon with
sides and (
vertices). It is clear that the number of sides of a polygon is always equal to the number of its vertices.
A polygon has interior angles. In the first figure below, angle measuring
degrees is an interior angle of polygon
. The angle sum
of
(not drawn to scale) is given by the equation
degrees.
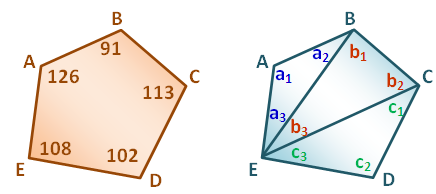
In the second figure, if we let and
be the measure of the interior angles of triangle
, then the angle sum m of triangle
is given by the equation
.
Angle Sum
To generalize our calculation of angle sum, we use the fact that the angle sum of a triangle is degrees. Notice that any polygon maybe divided into triangles by drawing diagonals from one vertex to all of the non-adjacent vertices. In the second figure above, the pentagon was divided into three triangles by drawing diagonals from vertex
to the non-adjacent vertices
and
forming
and
. Now let
and
, where
be measures of the interior angles of the three triangles as shown on the second figure.
Calculating the angle sum of pentagon we have
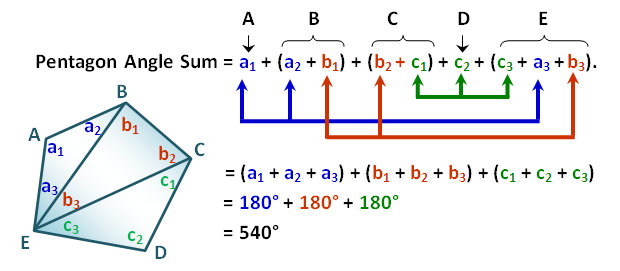
Notice that the angle measures in the first line of our equation is just a rearrangement of the measures of the interior angles of the three triangles. Hence, the angle sum of the pentagon is equal to the angle sum of the three triangles. Therefore, we can conclude that the sum of the interior angles of a polygon is equal to the angle sum of the number of triangles that can be formed by dividing it using the method described above. Using this conclusion, we will now relate the number of sides of a polygon, the number of triangles that can be formed by drawing diagonals and the polygon’s angle sum.
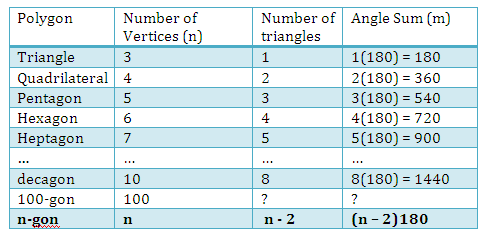
From the table above, we observe that the number of triangles formed is less than the number of sides of the polygon. This is true, because
triangles can be formed by drawing diagonals from one of the vertices to
non-adjacent vertices. Therefore, there the angle sum
of a polygon with
sides is given by the formula
A More Formal Proof
Theorem: The sum of the interior angles of a polygon with sides is
degrees.
Proof:
Assume a polygon has sides. Choose an arbitrary vertex, say vertex
. Then there are
non-adjacent vertices to vertex
. If diagonals are drawn from vertex
to all non-adjacent vertices, then
triangles will be formed. The sum the interior angles of
triangles is
. Since the angle sum of the polygon with
sides is equal to the sum the interior angles of
triangles, the angle sum of a polygon with
sides is
.
Exercises:
1.) Find the number the angle sum of a dodecagon (-sided polygon).
2.) The angle sum of a polygon is degrees. What is the number of its sides?
3.) The measure of one of the angles of a regular polygon is . Find its number of sides.
4.) From this, prove that the sum of the interior angles of a polygon is degrees.