Tag: introduction to area under the curve

Introduction

One of the most fundamental problems that gave birth to integral calculus was the calculation of areas bounded by curves. The Greeks used method of exhaustion to remedy this problem, particularly on finding the area of a circle. After Descartes’ and Fermat’s invention of Coordinate Geometry, algebraic solutions were utilized.

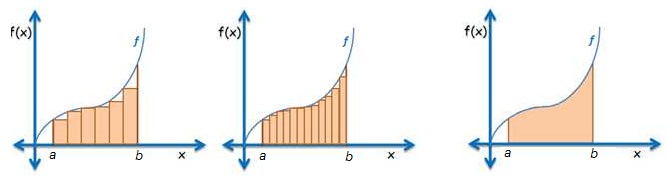
One of the strategies used to find the area under the function between and is to divide it into sub-intervals and form rectangles as shown in the first figure. Clearly, as the number of rectangles increases, the sum of all the areas of the rectangles gets closer and closer to the area of under the curve. » Read more