area under the curve Archives - Math and Multimedia

A Calculus Primer Part 2

November 7, 2012 GB High School Calculus, High School Mathematics

Introduction

In the first post in this series, we discussed about the graph of the speed over time of two cars, A and B. Car A was traveling at a constant speed from 2 to 3 o’clock, while Car B was traveling the same time but accelerating.

calculus primer

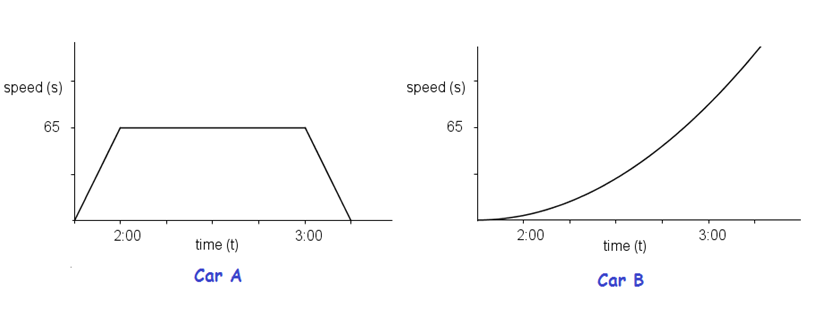
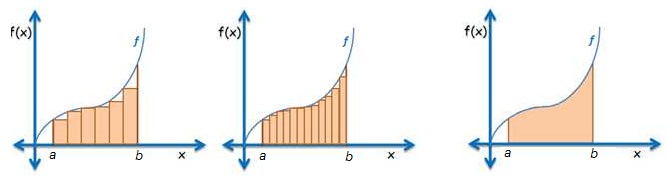
In the discussion, we learned that the distance traveled by the cars is represented by the area under their graphs, while acceleration is represented by slope of the line passing through two points on the graph. We ended our discussion with two questions: » Read more

One comment area under the curve, distance traveled by an accelerating object, integral calculus, method of exhaustion, riemann integral

Motion and Graphs: A Calculus Primer

November 4, 2012 GB High School Calculus, High School Mathematics

As I have stated in the introduction to Solving Motion Problems, a moving object discussed in elementary and middle schools are usually assumed to be at a constant speed. For example, a car traveling at 65 kilometers per hour is assumed to travel at the said speed the whole time. Of course, this is not what happens in reality. The car speeds up, slows down, or stops at times.

Click image to enlarge

The graphs of two cars traveling at different speeds (kilometers per hour) are shown above. Car A is traveling at a constant speed from 2:00 to 3:00 as shown in the first graph. Since the speed is constant, the graph is a horizontal line. The graph of the accelerating Car B is shown on the right. The car is accelerating, so the graph curves upward as it goes to the right. » Read more

2 comments area under the curve, motion problems, slope of a secant line, slope of a tangent line, speed and acceleration problems

Calculating the Area Under a Curve: An Intuitive Introduction

October 20, 2012 GB High School Calculus

Introduction

One of the most fundamental problems that gave birth to integral calculus was the calculation of areas bounded by curves. The Greeks used method of exhaustion to remedy this problem, particularly on finding the area of a circle. After Descartes’ and Fermat’s invention of Coordinate Geometry, algebraic solutions were utilized.

One of the strategies used to find the area under the function $f$ between $a$ and $b$ is to divide it into sub-intervals and form rectangles as shown in the first figure. Clearly, as the number of rectangles increases, the sum of all the areas of the rectangles gets closer and closer to the area of under the curve. » Read more

Leave a comment area under the curve, definite integral, introduction to area under the curve, riemann sums