PROBLEMS
1.) Find a linear function 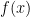 such that
such that 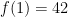 and
and 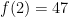 .
.
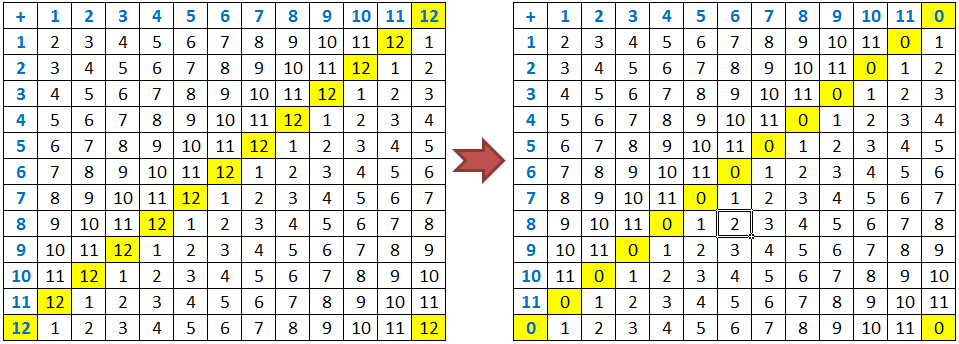
2.) Solve for  :
: 
3.) Prove that the product of 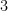 consecutive numbers is always divisible by
consecutive numbers is always divisible by 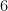 .
.
4.) Prove that if 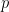 is prime,
is prime,  and
and 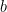 are integers, and
are integers, and  , then
, then 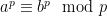 .
.
SOLUTIONS AND PROOFS
Post Date: October 20, 2009
1. Solution: This is just the same as saying, find the equation of the line passing through  and
and  . So, by point slope formula, we have,
. So, by point slope formula, we have, 
2.) Solution:
3.) Proof: A number is divisible by 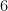 if it is divisible by
if it is divisible by 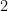 and
and 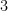 . A product of
. A product of 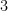 consecutive numbers is divisible by
consecutive numbers is divisible by 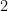 because at least one of them is even, so it remains to show it is divisible by
because at least one of them is even, so it remains to show it is divisible by 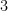 .
.
If a number is divided by 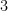 , its possible remainders are
, its possible remainders are 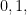 and
and 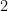 . Assume
. Assume  and
and  be the three consecutive numbers, and
be the three consecutive numbers, and  be the remainder if
be the remainder if  is divided by
is divided by 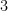 .
.
Case 1: If  , we are done.
, we are done.
Case 2: If 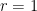 , then
, then 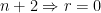
Case 3: If 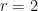 , then
, then 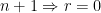 .
.
Since the product of the three consecutive numbers is even, and for each case of  , one of the consecutive numbers is divisible by
, one of the consecutive numbers is divisible by 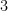 , the product of three consecutive numbers is divisible by
, the product of three consecutive numbers is divisible by 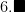
4.) Proof: From definition,  for some
for some 
Raising both sides of the equation to 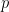 , we have
, we have  By the binomial theorem,
By the binomial theorem,  .
.
Notice that every term aside from 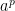 is divisible by
is divisible by 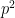 . (Why?). Therefore,
. (Why?). Therefore, 
Hence, then 

.