Tag: modular systems

The Clock Arithmetic and Modular Systems Series

High School Mathematics, High School Number Theory

This is a series of posts that explains modular systems starting from an intuitive introduction using clocks. I wrote this for high school students of average mathematical ability.

clock arithmetic

I hope you find the series easy to read and student friendly.

The Series

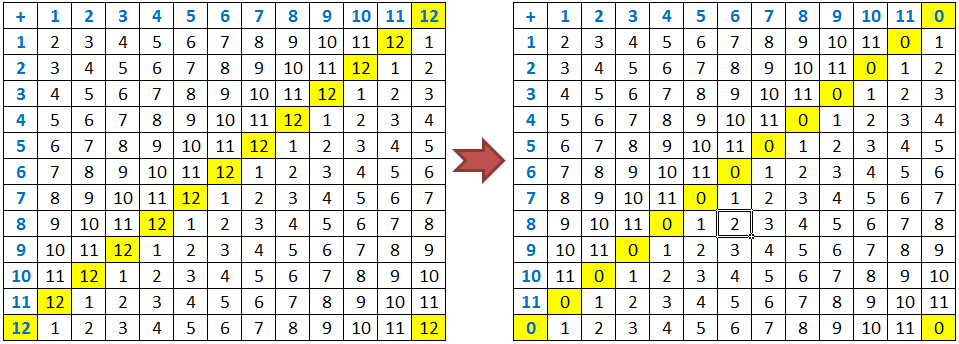
Part 1: Introduction to Clock Arithmetic and Modular Systems

This post introduces modular arithmetic intuitively using the 12-hour clock mathematical operations. What happens if we add the numbers on the clock? » Read more

One comment , , , ,

The Definition of Congruence in the Modular Systems

College Mathematics, Number Theory

This is the fourth part of the Introduction to the Modular Number Systems Series. In the previous parts, we have learned intuitively the modular systems using a 12-hour analog clock, performed operations with its numbers and introduce the symbol for congruence,  and discussed the different number bases.  In this post, we formally define congruence.

modular systems

image via Wikipedia

Recall that the statement 17 \equiv 5 (\mod 12) means that 17 gives a remainder of 5 when divided by 12, or that 17 and 5 give the same remainder when divided by 12. We have also learned that 17, 29, and 41 are congruent since all of them give the same remainder (that is 5) when divided by 12. Notice also that since all of them are congruent, » Read more

2 comments , , ,

Clock Arithmetic and Modular Systems Part 2

College Mathematics, Number Theory

This is the second part of the Introduction to Modular Systems Series. Please read the first part before proceeding.

Last Monday, we have learned a number system that uses numbers on the 12-hour analog clock. We have performed addition using these numbers and discovered that in that system, 12 behaves like 0. We have also observed that to add large numbers, we need to divide the number by 12 and get the remainder.

modulo-12

Recreating the table by replacing 12 with 0 gives us the second table in the figure above. As we can see, in this new number system, we have digits 0 through 11 as opposed 0 through 9 in the number system that we use everyday (the decimal number system).

In this new system, we have observed that there is a certain  number where numbers wrap around. The wrap around number is called the modulo. The modulo of our “clock number system” is 12, so we call it modulo 12. » Read more

9 comments , , ,