One of the most difficult proof strategies in mathematics is proof by contradiction. If P, for example, is a statement or a conjecture, one strategy to prove that P is true is to assume that P is not true and find a contradiction so that the statement not P does not hold. If not P does not hold, it follows that P is true.
One well-known proof that uses proof by contradiction is proof of the irrationality of 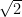 . If we consider P to be the statement “
. If we consider P to be the statement “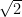 is irrational”, then not P is the opposite statement or “
is irrational”, then not P is the opposite statement or “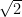 is rational”. To use proof by contradiction, we assume that
is rational”. To use proof by contradiction, we assume that 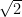 is rational, and find a contradiction somewhere. If this happens, then we would have shown that
is rational, and find a contradiction somewhere. If this happens, then we would have shown that 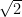 is indeed irrational.
is indeed irrational.
Before proceeding, recall that a rational number is a fraction with non-zero denominator. We know that all fractions can be expressed in lowest term. A fraction in  is said to be in lowest term if
is said to be in lowest term if  and
and 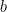 have no common divisors except
have no common divisors except 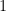 .
.
On the other hand, irrational numbers cannot be expressed as fractions. They are decimal numbers that do not end and do not repeat. For example,  is an irrational number (the three dots means and so on which means that the number does not end). The most popular irrational number is
is an irrational number (the three dots means and so on which means that the number does not end). The most popular irrational number is 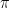 .
.
Now, we prove our conjecture.
Conjecture: The 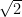 is irrational.
is irrational.
Proof:
Suppose 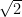 is rational, then it can be expressed in fraction form
is rational, then it can be expressed in fraction form  . Let us assume that our fraction is in lowest term, i.e., their only common divisor is
. Let us assume that our fraction is in lowest term, i.e., their only common divisor is 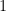 . Then,
. Then,

Squaring both sides, we have

Multiplying both sides by  yields
yields
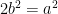 *
*
Since 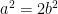 , we can conclude that
, we can conclude that 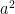 is even because whatever the value of
is even because whatever the value of  has to be multiplied by
has to be multiplied by 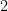 . If
. If 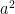 is even, then
is even, then  is also even. Since
is also even. Since  is even, no matter what the value of
is even, no matter what the value of  is, we can always find an integer that if we divide
is, we can always find an integer that if we divide  by
by 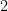 , it is equal to that integer. If we let that integer be
, it is equal to that integer. If we let that integer be 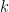 , then
, then  which means that
which means that  .
.
Substituting the value of 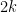 to
to  in *, we have
in *, we have 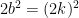 which means that
which means that 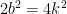 . Dividing both sides by
. Dividing both sides by 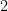 , we have
, we have  . That means that the value
. That means that the value  is even, since whatever the value of
is even, since whatever the value of 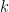 you have to multiply it by
you have to multiply it by 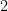 . Again, if
. Again, if  is even, then
is even, then 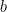 is even.
is even.
This implies that both  and
and 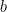 are even, which means that both the numerator and the denominator of our fraction are divisible by
are even, which means that both the numerator and the denominator of our fraction are divisible by 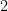 . This contradicts our assumption that
. This contradicts our assumption that  has no common divisor except
has no common divisor except 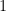 . Since we found a contradiction, our assumption is, therefore, false. Hence, the theorem is true.
. Since we found a contradiction, our assumption is, therefore, false. Hence, the theorem is true.
Notice that I have highlighted the word suppose and assume in the proof. This is one unique feature of proof by contradiction. You can always assume, most of the time, the opposite of the conjecture as long as the following statements are logically valid.
