slope intercept Archives - Math and Multimedia

Slope Concept 3 – Slopes of Vertical and Horizontal Lines

May 24, 2010 GB High School Algebra, High School Mathematics

Note: This is the third part of the Slope Concept Series.

Part II: Slope of the Graph of a Linear Function

In the Understanding the Basic Concepts of Slope post, we have discussed that the slope of a line in the coordinate plane is described as the change in y over the change in x. When we say change in x, or change in y, we talk about the ‘change distance.’ To determine a distance we need two points. If we are in the coordinate plane, and we have two points with coordinates $(x_1,y_1)$ and $(x_2,y_2)$ , then the rise is $y_2 - y_1$ and the run is $x_2 - x_1$ . Thus, the slope of the line containing the two points is $\displaystyle\frac{y_2-y_1}{x_2-x_1}$ .

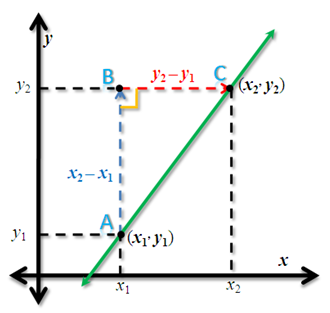
Fiigure 1 - Slope of a line containing points with coordinates (x1,y1) and (x2,y2).

We also have discussed that the slope of a horizontal line is 0 by rotation. Here, we will show the same fact using coordinates as shown.

A horizontal line has the same y-coordinates everywhere. Let us consider line l in Figure 2 with equation $y = a$ . Let us pick two points with coordinates $(x_1,a)$ and $(x_2,a)$ . Using the formula above, calculating for the slope we have $\displaystyle\frac{a -a}{x_2 - x_1} = \frac{0}{x_2 - x_1 }= 0$ . Hence, the slope of a horizontal line l is $0$ .

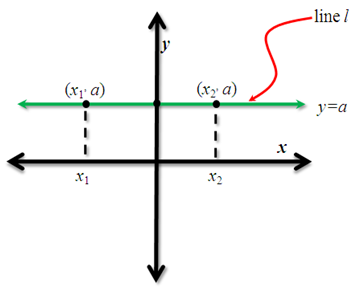
Figure 2 - A horizontal line containing points with coordinates (x_1,a) and (x_2,a)..

Similarly, a vertical line has the same x-coordinate everywhere. Let us consider line m in Figure 3 with equation $x = b$ . Let us pick two points with coordinates $(b,y_1)$ and $(b,y_2)$ . Using the formula above, calculating the slope, we have $\displaystyle\frac{y_2 - y_1}{b - b} = \frac{ y_2 - y_1}{0}$ which is undefined.