zero slope Archives - Math and Multimedia

Slope Concept 3 – Slopes of Vertical and Horizontal Lines

May 24, 2010 GB High School Algebra, High School Mathematics

Note: This is the third part of the Slope Concept Series.

Part II: Slope of the Graph of a Linear Function

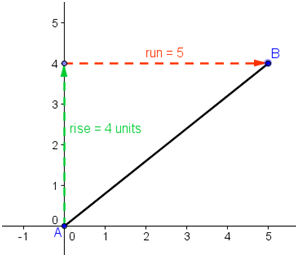
In the Understanding the Basic Concepts of Slope post, we have discussed that the slope of a line in the coordinate plane is described as the change in y over the change in x. When we say change in x, or change in y, we talk about the ‘change distance.’ To determine a distance we need two points. If we are in the coordinate plane, and we have two points with coordinates $(x_1,y_1)$ and $(x_2,y_2)$ , then the rise is $y_2 - y_1$ and the run is $x_2 - x_1$ . Thus, the slope of the line containing the two points is $\displaystyle\frac{y_2-y_1}{x_2-x_1}$ .

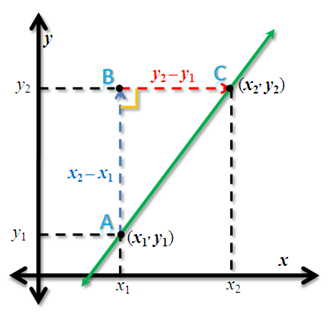
Fiigure 1 - Slope of a line containing points with coordinates (x1,y1) and (x2,y2).

We also have discussed that the slope of a horizontal line is 0 by rotation. Here, we will show the same fact using coordinates as shown.

A horizontal line has the same y-coordinates everywhere. Let us consider line l in Figure 2 with equation $y = a$ . Let us pick two points with coordinates $(x_1,a)$ and $(x_2,a)$ . Using the formula above, calculating for the slope we have $\displaystyle\frac{a -a}{x_2 - x_1} = \frac{0}{x_2 - x_1 }= 0$ . Hence, the slope of a horizontal line l is $0$ .

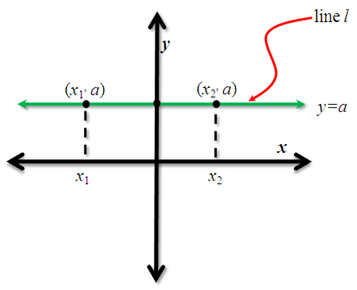
Figure 2 - A horizontal line containing points with coordinates (x_1,a) and (x_2,a)..

Similarly, a vertical line has the same x-coordinate everywhere. Let us consider line m in Figure 3 with equation $x = b$ . Let us pick two points with coordinates $(b,y_1)$ and $(b,y_2)$ . Using the formula above, calculating the slope, we have $\displaystyle\frac{y_2 - y_1}{b - b} = \frac{ y_2 - y_1}{0}$ which is undefined.

Figure 3 - A horizontal line containing points with coordinates (b,y2) and (b,y1).

In the sequel of this post, we will discuss the lines with positive and negative slopes.

3 comments slope formula, slope intercept, slope of a horizontal line, slope of a vertical line, undefined slope, zero slope

Slope Concept 1 – Understanding the Basic Concepts of Slope

April 13, 2010 GB High School Algebra, High School Mathematics

Note: This is the first part of the the Slope Concept Series. The sequels of this article are Part II – Slope of the Graph of a Linear Function and Part III – Slopes of Vertical and Horizontal Lines.

***

The slope is known to be the steepness of a line. Sometimes it is described as “rise over run,” If we are on point A, we go up 4 units and we go right 5 units (see Figure 1) then our rise is 4 and our run is 5. Let us mark our new location B. Notice that the order of movements does not matter. We can also go 5 units right and 4 units up and you will still be in B (see Figure 2).

If we do our movement in the coordinate plane starting from the origin, our rise would be our vertical movement (change of movement with respect to the y-axis) and our run would be our horizontal movement (change of movement with respect to the x-axis). In Figure 2, segment AB has rise 4 and run 5. Thus, the slope of segment AB is $\displaystyle\frac{4}{5}$ . In general, slope in the coordinate plane is described as the change in y over the change in x.

Figure 1 - Segment AB with rise 4 units and run 5 units.

The slope of a line (or a segment) may also be described as the angle it makes with a horizontal line. Technically speaking, it is a counterclockwise rotation with the line starting from a horizontal position about a point which is located on that line, or the origin our case. In Figure 2, $\theta$ is the angle measure AB makes with the horizontal axis of the rectangular coordinate plane, or the amount of rotation from AB’ to AB about A.

Figure 2 - Counter-clockwise rotation of AB to AB' about A.

Looking at triangle ABC, since the given sides are the side adjacent and the side opposite to $\theta$ , we can use the definition of tangent to compute for the value of $\theta$ . Recall from trigonometry that the definition of a tangent of an angle of a right triangle is equal to the quotient of the length of the side opposite to it (change in y) and the length of the side adjacent to it (change in x). Now, this is precisely the definition of slope. From here, we can conclude that the angle that a line makes with a horizontal line is the same as the slope of that line. As a consequence $\tan(\theta) = \displaystyle\frac{4}{5}$ in radian measure (or approximately 38 degrees) is the slope of the line.

Figure 3 - Triangle ABC with Slope 4/5.

If we examine the value of $\theta$ , it is clear that when $\tan(\theta)$ is $0$ degrees, the line is horizontal since there is no (zero) change in y. Algebraically, this makes the numerator of the fraction change in y $0$ which implies that the slope of any horizontal line is $0$ .

If the line is vertical, there is no (zero) change in x. That makes the denominator of the fraction change in x $0$ . Of course, we know that anything divided by $0$ is not defined. As a consequence, slope of a vertical line is undefined.

In the continuation of this article, we will discuss further about the properties of slope. We will discuss why the slope of a straight line is constant. We will further discuss zero, undefined, negative and positive slopes. We will also discuss how the concept of slope helps in solving calculus problems and how it is used to determine the behavior functions.

9 comments amount of rotation, change in y over change in x, coordinate plane, definition of slope, finding slope, rise over run, slope equation, slope formula, slope math, slope of a horizontal line, slope of a straight line, slope of a vertical line, steepness of a line, tangent of an angle, undefined slope, zero slope