Month: May 2010

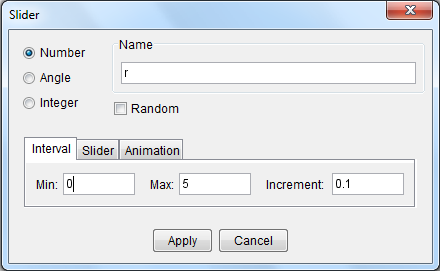
Counting the Uncountable: A Glimpse at Infinite Sets

College Mathematics, Set Theory

When counting, we pair the counting numbers (positive integers) with the objects that we are counting.  For example, when we count our fingers, we assign a corresponding number to each finger.  A possible assignment would be 1 to the pinkie, 2 to the ring finger, 3 to the middle finger, 4 to the index finger, and 5 to the thumb. Of course, the order does not matter as long as we have a one-to-one pairing. As we can see, counting is easy once the objects that we are counting is finite.

Higher mathematics, however, does not just deal with finite number of objects. Sometimes, mathematicians need to examine sets of objects with infinite number of elements.  Such sets are called infinite sets. The set of integers Z and the set of counting numbers N are examples of infinite sets.

One strategy used  to examine the number of elements in an infinite set is to find another infinite set that is easier to enumerate, then compare them.  If a strategy can be done such that each element in the first set can be paired with exactly one element in the second set without missing anything, then it follows that the two sets have the same number of elements.

http://assets.nydailynews.com/img/2008/03/01/alg_shoes.jpg

alg_shoes.jpg (JPEG Image, 450×321 pixels) via kwout

This may sound a little absurd at first, but let us have the following analogy:  If we want to know how many pairs of shoes are available in a shoe store, we do not have to count all the shoes.  We can just count the number of left-foot shoes, and we will know how many shoes are there. Our assumption, of course, is that every shoe has a pair.

Table 1 – Counting Numbers and Integers Pairing

With the abovementioned strategy, let us try to compare the set of counting numbers N and the set of the integers Z.  In Table 1, it is clear each element in N can be paired with exactly one element in Z, such that N is in increasing order and Z in alternating positive an negative signs. As we  can see, this strategy will not miss any integer as N increases without bound.   It is also apparent that even if the pairing continues forever, we are sure that each element in N has a pair in Z. Hence, the number positive integers N is the same as the number of all the integers Z including 0 and negative!

Surprised?

This is also the same with rational numbers. The number of elements in the set of positive rational numbers Q is the same as the number elements in the set of counting numbers N.  In Table 2, we can see the first 15 pairs of the one-to-one pairing.  There are duplicates such as 1/2 and 2/4, but we can easily eliminate equivalent fractions and replace them with the next rational numbers.  From the table, it is easy to see that we can devise a way to pair the set N (red texts) with the set Q (yellow texts) without missing anything.

Can you see the pattern?

Therefore, we can conclude that the number of positive rational numbers are as many as the number of counting numbers.

Table 2 – Counting numbers and rational numbers pairing.

From our discussion above, we can conclude that the set of counting numbers N, the set of integers Z, and the set of rational numbers Q have the same number of elements.

Going Technical

In set theory, the number of elements of a set is called cardinality.  Hence the cardinality of the set of vowel letters in the English alphabet {A, E, I, O, U} is 5, and the cardinality of the set of binary numbers {1,0} is 2.

Venn Diagram of the set of N, Z and Q.

It is interesting to note that there is a little bit of irony in our discussion above. We know that N is a subset of Z, and Z is a subset of Q, yet the three sets have the same cardinality.

The symbol \aleph_0  (or aleph null) is the symbol assigned to the cardinality of counting numbers.

Leave a comment , , ,

GeoGebra Tutorial 14 – Sliders and Circle-Area Approximation

GeoGebra, Software Tutorials

This is the 14th tutorial in the GeoGebra Tutorial Series. If this is your first time to use GeoGebra, I suggest that you read the GeoGebra Essentials series first.

In this tutorial, we use GeoGebra to approximate the area of a circle.  This strategy of approximating the area of a circle was used by the Greek mathematician Archimedes.

Since this tutorial is long, we split it into two parts. In Part I, we inscribe a regular polygon in a circle, increase its number of sides, and investigate the relationship between the areas. In Part II we will circumscribe the circle with a regular polygon increase its number of sides to approximate the circle’s area.  Before following the tutorial step-by-step, click here to view the final output.

Part I – Creating an Inscribed Polygon

Step-by-Step Instructions

1. Open GeoGebra click on Algebra & Graphics in the Perspectives menu. 
2. In this tutorial, we want all new objects to be labeled. To do this, click the Options menu, click Labeling, then click on All New Objects.
3. Next, we create  slider r that will determine the radius of the circle that we are about to create.  Select the Slider tool, then click anywhere on the Graphics view to display the Slider dialog box.
4. In the Slider dialog box, type r in the Name box, type 0.1 in the min box, and leave the max value as 5 and increment as 0.1, then click the Apply button.
5. Create another slider name it n, set the minimum to 3, maximum to 30 and increment to 1. Slider n will determine the number of sides of the inscribed polygon.
6. Next, we create point A on the origin. To do this, select the Intersect Two Objects Tool, click the x-axis and then click the y-axis.
7. To construct a circle with center A and radius r, type circle[A,r] . Move slider r and observe what happens.
8. To construct point B which is the intersection of the circle and the x-axis, type B = (r,0) in the input box and press the ENTER/RETURN key on the keyboard.
9. Now, we compute for the central angle of the inscribed polygon. To do this, we divide 360 by n. For example, if we want to have an equilateral triangle, we must divide 360 by 3, which will be the central angle. To do this, type a = (360/n)° then press the ENTER key. The degree sign, tells GeoGebra that a is an angle measure. You can display the ° sign can be written by clicking the \alpha button at the right of the input box.
10.  To create angle BAB’, click the Angle with Given Size tool, click on point B and then click on point A. This will display the Angle with Given Size dialog box.
11.  In the Angle dialog box, type a in the Angle text box,  choose the counterclockwise option, and then click the OK button. If you set r to 3, your drawing should look like the one shown in Figure 2.

Figure 2 – Central angle BAB’.
12.  To hide the angle measure (green sector), right click it then click Show Object.
13.  To construct the inscribed polygon, select the Regular Polygon tool, click B and then click B’. This will display the Regular Polygon dialog box.
14.  In the Regular Polygon dialog box, type n and then click the OK button. Now, drag slider n and see what happens. If you set n to 30 and a to 3, the figure should look like Figure 3.

Figure 3 – A circle with an inscribed 30-sided polygon.
15.  The problem now is to hide the labels of all the points and the segments. With n set to 30, right click the polygon, then click Object Properties from the context menu to display the Preferences dialog box.
16.  In the Preferences dialog box, select the Basic tab, click Point (be sure that the Point text is highlighted) in the Objects list, and uncheck the Show Label check box. This will hide the labels of all the points. Now, click Segment text in the Objects check box and uncheck the Show Label check box to hide the labels of all the sides of the polygons, then click the Close button.

GeoGebra Preferences Dialog Box

Figure 4 – The GeoGebra Preferences dialog box.

Exercise:

  1. Move the slider and observe what happens.
  2. Using the text tool, display the area of the circle and the area of the inscribed triangle.Your drawing should look like Figure 5.

Figure 5 – Final Output

10 comments , , , ,
1 … 3 4 5 6