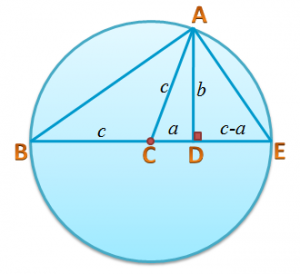
Using Similarity to Prove the Pythagorean Theorem

May 21, 2012 GB High School Geometry

The Pythagorean Theorem is one of the most interesting theorems for two reasons: First, it’s very elementary; even high school students know it by heart. Second, it has hundreds of proofs. The proof below uses triangle similarity.

Pythagorean Theorem

In a right triangle with side lengths $a$ and $b$ and hypotenuse $c$ , the following equation always holds:

$c^2 = a^2 + b^2$ .

Proof

In the figure above, triangle $BDA$ is similar to triangle $ADE$ . In similar triangles, the corresponding sides are proportional. It follows that

$\displaystyle\frac{BD}{AD} = \frac{AD}{DE}$

which is equivalent to

$\displaystyle\frac{c + a}{b} = \frac{b}{c-a}$ .

Cross multiplying, we have $c^2 - a^2 = b^2$ . Adding $a^2$ to both sides of the equation, we have $c^2 = a^2 + b^2$ , which is what we want to prove.

2 comments pythagoras theorem proof, pythagorean theorem, pythagorean theorem proof, triangle similarity

Using Similarity to Prove the Pythagorean Theorem

Leave a ReplyCancel reply