A Calculus Primer Part 3

This is the third part and the conclusion to the Mathematics and Multimedia’s Calculus Primer Series. The first part can be read here and the second part can be read here.

In the previous part of this series, we have discussed how mathematicians of the ancient times found clever ways to find the area of regions bounded by curves. We used this knowledge to generalize a way to solve the distance traveled by an accelerating car. In this post, we continue with the discussion of the second problem: How do we find the acceleration of the car at a particular instance?

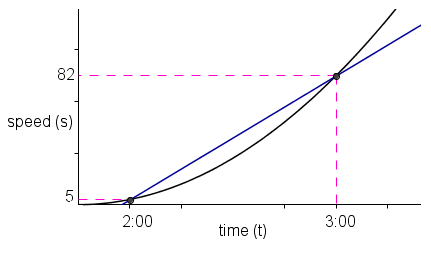
Recall that in the problem, at 2 o’clock, the speed of the car is 5 kilometers per hour and at 3 o’clock, its speed is 120 kilometers per hour. So, the acceleration is 77 km/hr/hr.

The question that we want to solve was how much was the car accelerating at exactly 2:30. Our hint in the first part of this series was the relationship between the acceleration of Car B and its graph. We discovered that the acceleration equals the slope of the line passing through two points on the graph.  Consequently, in solving the problem, we have to find the slope of the line passing through (2:30,s) where s is the speed of Car B at that particular instant. Now, there are infinitely many lines that can pass a single point, so  which line are we looking for?

Also, note that difference means subtracting two quantities, but our problem is we only have one time and one speed at 2:30, which means that we cannot use the formula.

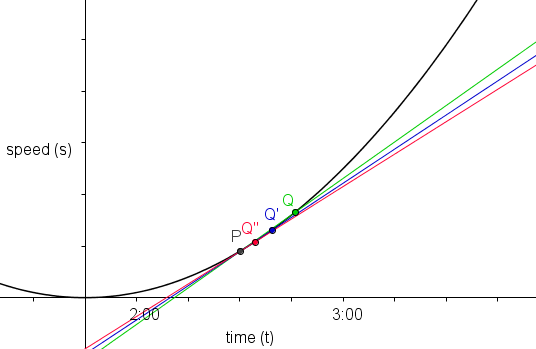
To approximate the slope of the graph, first we create point P on the graph with x-coordinate as 2:30. Then, we create point Q on the graph near P. The slope of line PQ is almost the same as the slope of the line passing through P. Notice that if we move Q towards P, as shown by Q’ and Q” in the second figure, the slope of PQ approaches the slope of the line passing through P.  From this illustration, we can see that the line that we are looking for is the line tangent to the graph and passing through P.  In effect, if we can find the slope of this line, we determine the acceleration of the car during that particular instant (2:30).

Technically, we say that the limit of the slope line PQ as Q approaches P is equal to the slope of the line tangent to the graph passing through P.

The problem above and the outline of its solution that you have read gave birth to Differential Calculus. I will not delve on the technical details of the solution because I have already discussed it in the Algebraic and Geometric Meaning of Derivative.

Summary

In this 3-part series, we have seen the connection between two concepts, limits and approximation. We have also discovered the connection between Differential and Integral Calculus. In addition, we have seen that some of the important development of mathematics came from the need to solve particular problems. The most important thing this lesson taught us is some problems are so important that solving them sometimes gives birth to new ideas or even new mathematics.