Why Every Proof that 0.999… = 1 is Wrong
The proof made me look at the ceiling (lol). It sounded very convincing for a few seconds. Watch and watch closely til the end.
School math, multimedia, and technology tutorials.
The proof made me look at the ceiling (lol). It sounded very convincing for a few seconds. Watch and watch closely til the end.
Introduction
Yes it is. 0.999… is equal to 1.
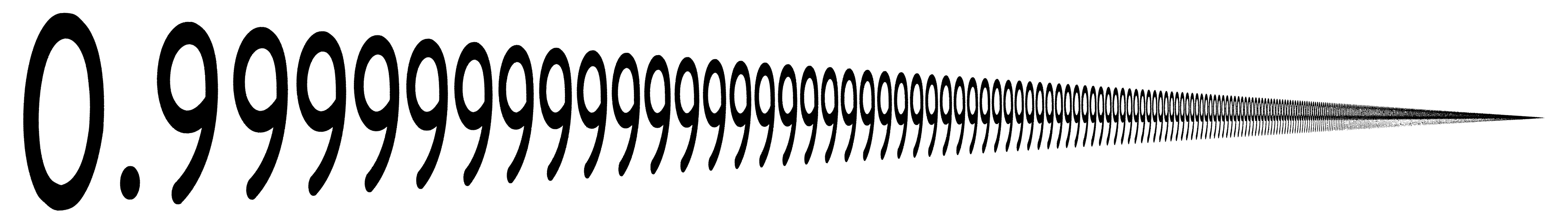
Before we begin our discussion, let me make a remark that the symbol “…” in the decimal 0.999… means that the there are infinitely many 9’s, or putting it in plain language, the decimal number has no end.
For non-math persons, you will probably disagree with the equality, but there are many elementary proofs that could show it, some of which, I have shown below. A proof is a series of valid, logical and relevant arguments (see Introduction to Mathematical Proofs for details), that shows the truth or falsity of a statement.
Proof 1
But , therefore
Proof 2
Multiplying both sides by 9 we have
Proof 3
Let
Hence,
Still in doubt?
Many will probably be reluctant in accepting the equality because the representation is a bit counterintuitive. The said equality requires the notion of the real number system, a good grasp of the concept of limits, and knowledge on infinitesimals or calculus in general. If, for instance,you have already taken sequences (in calculus), you may think of the
as a sequence of real numbers
. Note that the sequence gets closer and closer to 1, and therefore, its limit is 1.
Infinite Geometric Sequence
My final attempt to convince you that is indeed equal to
is by the infinite geometric sequence. For the sake of brevity, in the remaining part of this article, we will simply use the term “infinite sequence” to refer to an infinite geometric sequence. We will use the concept of the sum of an infinite sequence, which is known as an infinite series, to show that
.
One example of an infinite series is . If you add its infinite number of terms, the answer is equal to 1. Again, this is counterintuitive.
How can addition of numbers with infinite number of terms have an exact (or a finite) answer?
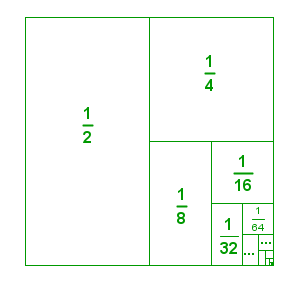
There is a formula to get the sum of an infinite geometric sequence, but before we discuss the formula, let me give the geometric interpretation of the sum above. The sum can be represented geometrically using a 1 unit by 1 unit square as shown below. If we divide the square into two, then we will have two rectangles, each of which has area
square units. Dividing the other half into two, then we have three rectangles with areas
,
,
square units. Dividing the one of the smaller rectangle into two, then we have four rectangles with areas
,
,
,
. Again, dividing one of the smallest rectangle into two, we have five rectangles with areas
,
,
,
, and
Since this process can go on forever, the sum of all the areas of all the rectangles will equal to 1, which is the area of the original square.
Now that we have seen that an infinite series can have a finite sum, we will now show that can be expressed as a finite sum by expressing it as an infinite series. The number
can be expressed as an infinite series
. Converting it in fractional form, we have
.
We have learned that the sum of the infinite series with first term and ratio
is described by
. Applying the formula to our series above, we have
Therefore, the sum our infinite series is 1.
Implication
This implication of the equality means that any rational number that is a non-repeating decimal can be expressed as a repeating decimal. Since
, it follows that
and so on. Hence, any decimal number maybe expressed as number + 0.00…01. For example, the decimal
, can be expressed as
. The number
can also be expressed as
Conclusion
Any of the four proofs above is actually sufficient to show that . Although this concept is quite hard to accept, we should remember that in mathematics, as long as the steps of operations or reasoning performed are valid and logical, the conclusion will be unquestionably valid.
There are many counterintuitive concepts in mathematics and the equality is only one of the many. In my post, Counting the Uncountable: A Glimpse at the Infinite, we have also encountered one: that the number of integers (negative, 0, positive) is equal to the number of counting numbers (positive integers) and we have shown it by one-to-one pairing. We have also shown that the number of counting numbers is the same as the number of rational numbers. Thus, we have shown that a subset can have the same element as the “supposed” bigger set. I guess that is what makes mathematics unique; intuitively, some concepts do not make sense, but by valid and logical reasoning, they perfectly do.
Notes: