definition of limits Archives - Math and Multimedia

An extensive explanation about the Epsilon-Delta definition of limits

March 15, 2010 GB Calculus and Analysis, College Mathematics

One of the most important topics in elementary calculus is the $\epsilon-\delta$ definition of limits. The definition says that the $\lim_{x \to a} f(x)= L$ if and only if, for all $\epsilon > 0$ , there exists a $\delta >0$ such that if $|x-a| < \delta$ , then $|f(x) - L |<\epsilon$ . In this article, we are going to discuss what this definition means. Readers of this article must have knowledge about elementary calculus and the concept of limits.

Review of Limit Basics

Consider the function $f(x) = 2x$ . We have learned from elementary calculus that $\lim_{x \to 2} 2x = 4$ . Aside from algebraic computation, this is evident from the color-coded graph and the table shown in Figure 1. The yellow arrows in the graph and the values in the yellow cells in the table indicate that as the value of $x$ approaches $2$ from the left of the x-axis, the value of $f(x)$ approaches $4$ from below of the y-axis. On the other hand, the red arrows in the graph and the values in the red cells in the table indicate that as the value of $x$ approaches $2$ on from the right of the x-axis, the value of $f(x)$ approaches $4$ from above of the y-axis.

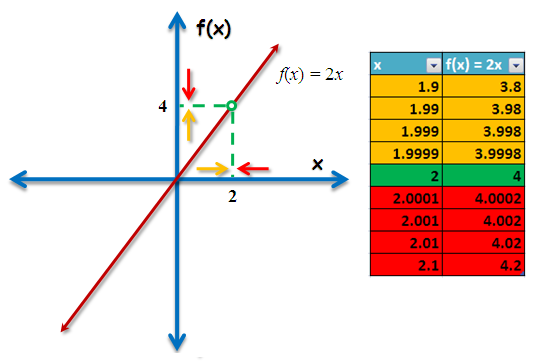
Figure 1 – The table and the graph showing the value of f(x) as x approaches 2 from both sides.

From the above discussion, it is noteworthy to mention three things:

We can get $f(x)$ as close to $4$ as we please by choosing an $x$ sufficiently close to $2$ . For example, I can set $x$ to $1.9999 \cdots99$ (with $100$ nines) to get an $f(x)$ very close to $4$ , which is $3.9999 \cdots 98$ ( $99$ nines).
No matter how small is the distance of $x$ from $2$ , a distance less than it may still be chosen. For example, if we choose the point which is very close to $2$ , say a point with coordinate $1.9999 \cdots 99$ with ( $100$ nines), we can still choose a value closer than this to $2$ . For instance, we can choose $1.9999 \cdots 99$ with $101$ nines. This can be repeated for every chosen distance.
Although $x$ can be very very close to $2$ , it does not necessarily mean that $x$ equals $2$ .

Now we go back to the definition of limits. In a specific example, the limit definition states that the $\lim_{x \to 2} 2x = 4$ if (and only if) for all distance (denoted by the Greek letter $\epsilon$ ) from $4$ along the y-axis (directly above or below $4$ ) – no matter how small – we can always find a certain distance (denoted by $\delta$ ) from $2$ along the x-axis (left or right of $2$ ) such that if $x$ is between $2 - \delta$ and $2 + \delta$ , then $f(x)$ would lie between $4 - \epsilon$ and $4 + \epsilon$ .

To give you a more concrete example, suppose we want the distance $\epsilon$ from $4$ , which is our limit, to be $0.1$ then the interval of our $f(x)$ is ( $4 -0.1, 4+ 0.1) = (3.9,4.1)$ . The definition of limit says that given a distance $\epsilon = 0.1$ , we can find a distance $\delta$ in the x-axis such that if $x$ is between $2 - \delta$ and $2 + \delta$ , we are sure that $f(x)$ is between $3.9$ and $4.1$ . We do not know the value of $\delta$ yet, but we will calculate it later.

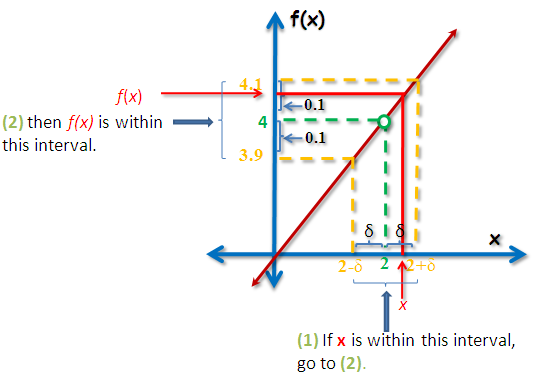
Figure 2 – The epsilon-delta definition given epsilon = 0.1.

In Figure 2, $x$ is between $2 - \delta$ and $2 + \delta$ or $2 - \delta < x < 2 + \delta$ . Subtracting $2$ from all terms of the inequality, we have $- \delta < x - 2 < \delta$ . If you recall the definition of absolute value, this is precisely the same as $|x - 2| < \delta$ . The comparison among the notations is in Table 1.

Using the notations in the table, we can conclude that the following statements are equivalent:

Words: Given $\epsilon = 0.1$ , we can find a $\delta$ such that if $x$ is between $2 - \delta, 2 + \delta$ , then $f(x)$ is between $3.9$ and $4.1$ .
Set Notation: Given $\epsilon = 0.1$ , we can find a $\delta$ such that if $x \in (2 -\delta, 2 + \delta)$ , then $f(x) \in (3.9,4.1)$ .
Relational Operator: Given $\epsilon = 0.1$ , we can find a $\delta$ such that if $2 - \delta < x < 2 + \delta$ , then $3.9< f(x) < 4 .1$ .
Absolute Value: Given $\epsilon = 0.1$ , we can find a $\delta$ such that if $|x-2| < \delta$ , then $|f(x) - 4| < 0.1$ .

We have discussed that we can get $f(x)$ as close to $4$ as we please

by choosing an $x$ sufficiently close to $2$ . This is equivalent to choosing an extremely small $\epsilon$ , no matter how small, as long as $\epsilon>0$ . Our next task is to find the $\delta$ that corresponds to that $\epsilon$ .

Applying this definition to our example, we can say the $\lim_{x \to 2} 2x = 4$ if and only if, given $\epsilon > 0$ (any small distance above and below 4), we can find a $\delta > 0$ (any distance from x to the left and right of $2$ ) such that if $|x - 2| < \delta$ , then $|f(x) - 4| < \epsilon$ .

The Definition of a Limit of a Function

Now, notice that $4$ is the limit of the function as $x$ approaches $2$ . If we let the limit of a function be equal to $L$ and $a$ be the fixed value that $x$ approaches, then we can say that $\lim_{x \to a} f(x) = L$ if and only if, for any $\epsilon>0$ (any small distance above and below $L$ ), we can find a $\delta>0$ (any small distance from to the left and to the right of a) such that if $|x - a| < \delta$ then, $|f(x) - L| < \epsilon$ . And that is precisely, the definition of limits that we have stated in the first paragraph of this article.

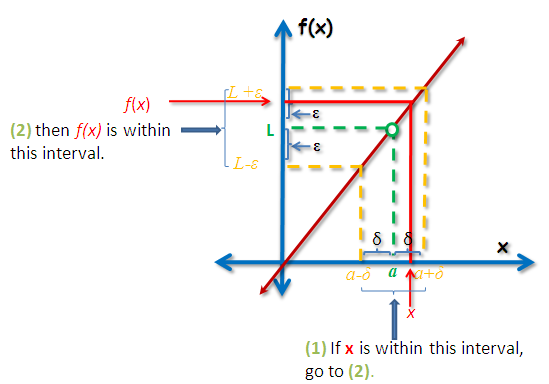
Figure 3 – The epsilon-delta definition given any epsilon.

In mathematics, the phrase “for any” is the same as “for all” and is denoted by the symbol $\forall$ . In addition, the phrase “we can find” is also the same as “there exists” and is denoted by the symbol $\exists$ . So, rephrasing the definition above, we have $\lim_{x \to a} f(x) = L$ if and only if, $\forall \epsilon > 0, \exists \delta >0$ , such that if $|x - a| < \delta$ then, $|f(x) - L| < \epsilon$ . A much shorter version of this definition is the phrase $\lim_{x \to a} f(x) = L \iff, \forall \epsilon > 0, \exists \delta >0$ , such that $|x - a| < \delta \Rightarrow |f(x) - L| < \epsilon$ . The symbol $\iff$ stands for if and only if and the symbol $\Rightarrow$ is similiar to if-then. If $P$ and $Q$ are statements, the statement $P \Rightarrow Q$ is the same as the statement of the form “If $P$ then $Q$ “.

Finding a specific delta

We said that given any positive $\epsilon$ , we can find a specific $\delta$ , no matter how small our $\epsilon$ is. So let us try our first specific value $\epsilon = 0.1$ .

From the definition, we have $\lim_{x \to 2} 2x = 4$ if and only if, given $\epsilon> 0$ (any small distance above and below 4), $\exists \delta >0$ such that if $|x -2| < \delta$ then, $|f(x) - 4| < \epsilon$ .

Now $|f(x) - 4| = |2x - 4| < \epsilon$ . This implies that
$|2||x-2| < \epsilon$ which implies that $2|x - 2| <0.1$ . Simplifying, we have $|x- 2| < 0.05$ . This means that our $x$ should be between $1.95$ and $2.05$ to be sure that our $f(x)$ is between $3.9$ and $4.1$ . This is shown in Figure 4.

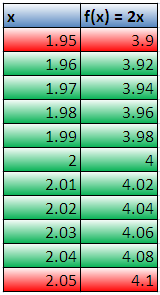
Figure 4 – The table showing some of the values of epsilon and delta satisfying the definition of limit of 2x as x approaches 2.

Now, let $\epsilon = 0.05$ . This means that our interval is $(3.95,4.05)$ . Now $|f(x) - 4| = |2x - 4| < 0.05$ . Thus, $|2||x -2| < \epsilon$ which implies that $2|x - 2| <0.05$ . Solving, we have $|x - 2| < 0.025$ . This means that our $x$ should be between $1.975$ and $2.025$ to be sure that our $f(x)$ is between $3.95$ and $4.05$ . There are only two examples above, but the definition tells us that we can choose any $\epsilon > 0$ so let us generalize our statement by doing so.

Now $|f(x) - 4| = |2x - 4| < \epsilon$ . This results to $|2||x -2| < \epsilon$ which implies that $2|x - 2| <\epsilon$ . Solving, we have $|x - 2| < \epsilon/2$ . From the condition above, $|x - 2| < \delta$ so we can let $\delta = \epsilon/2$ .

This means given any $\epsilon$ , we just let our $\delta$ equal to $\epsilon/2$ and we are sure that if $x$ is between $2-\delta/2$ and $2+\delta$ to be sure that our $f(x)$ is between $4 - \epsilon$ and $4 - \epsilon$ .