Division by Zero
In studying mathematics, you have probably heard that division of zero is undefined. What does this mean?
Since we do not know exactly what is the answer when a number is divided by 0, it is probably reasonable for us to examine the quotient of a number that is divided by a number that is close to 0.
If we look at the number line, the numbers close to 0 are numbers numbers between –1 and 1.

Figure 1 – The number line showing the numbers close to 0.
For instance, several positive numbers close to 0 and less than 1 are 0.1, 0.01, 0.001 and so on. Similarly, negative numbers close to 0 but greater than – 1 are –0.1, -0.01, -0.001 and so on.
The table and the numbers below shows the quotient 1/x when 1 is divided by x, where the x’s are numbers close to 0.
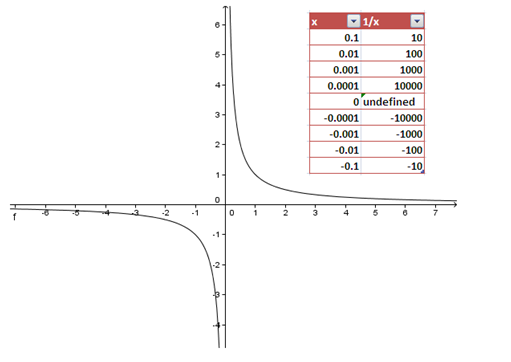
Figure 2 – The value of 1/x as x approaches 0 from both sides.
In the graph, as x approaches 0 from the right (as x, where x are positive numbers, approach 0), the quotients of 1/x are getting larger and larger. On the other hand, as x approaches 0 from the left (as x, where x are negative numbers, approach 0), 1/x is getting smaller and smaller. Hence, there is no single number that 1/x approach as x approaches 0. For this reason, we say that 1/0 is undefined.
A simple analogy would also let us realize that allowing division by 0 will violate an important property of real numbers. For example 8/4 = 2 because 2 x 4 = 8. Assuming division of 0 is allowed. If 5/0 = n, then n x 0 = 5. Now, that violates the property of a real number that any number multiplied by 0 is equal to 0.
Since division by 0 yields an answer which is not defined, the said operation is not allowed.
Related Posts