October 2009 - Math and Multimedia

Sum of the interior angles of a polygon

October 21, 2009 GB High School Geometry, High School Mathematics, Questions and Quandaries

We were taught that if we let $m$ be the angle sum (the total measure of the interior angles) and $n$ be the number of vertices (corners) of a polygon, then $m = 180(n-2)$ . For example, a quadrilateral has $4$ vertices, so its angle sum is $180(4-2) = 360$ degrees. Similarly, the angle sum of a hexagon (a polygon with $6$ sides) is $180(6-2) = 720$ degrees.

But where did this formula come from? Does this formula work for all polygons? (Note that in this discussion, when we say polygon, we only refer to convex polygons).

Before we answer these questions, let us first have a brief review of some elementary concepts.

Polygons and Interior Angles

A polygon is a closed figure with finite number of sides. In the figures below, $ABCDE$ is a polygon with $5$ sides and ( $5$ vertices). It is clear that the number of sides of a polygon is always equal to the number of its vertices.

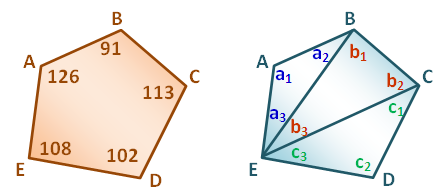
A polygon has interior angles. In the first figure below, angle $B$ measuring $91$ degrees is an interior angle of polygon $ABCDE$ . The angle sum $m$ of $ABCDE$ (not drawn to scale) is given by the equation

$m = 126 + 91 + 113 + 102 + 108 = 540$ degrees.

twopentagons

In the second figure, if we let $a_1, a_2$ and $a_3$ be the measure of the interior angles of triangle $ABE$ , then the angle sum m of triangle $ABE$ is given by the equation $m = a_1 + a_2 + a_3$ .

Angle Sum

To generalize our calculation of angle sum, we use the fact that the angle sum of a triangle is $180$ degrees. Notice that any polygon maybe divided into triangles by drawing diagonals from one vertex to all of the non-adjacent vertices. In the second figure above, the pentagon was divided into three triangles by drawing diagonals from vertex $E$ to the non-adjacent vertices $B$ and $C$ forming $BE$ and $CE$ . Now let $a_k, b_k$ and $c_k$ , where $k = 1, 2, 3$ be measures of the interior angles of the three triangles as shown on the second figure.

Calculating the angle sum of pentagon $ABCDE$ we have

pentagonanglesum

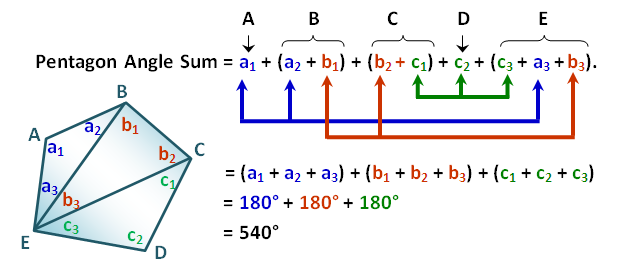
Notice that the angle measures in the first line of our equation is just a rearrangement of the measures of the interior angles of the three triangles. Hence, the angle sum of the pentagon is equal to the angle sum of the three triangles. Therefore, we can conclude that the sum of the interior angles of a polygon is equal to the angle sum of the number of triangles that can be formed by dividing it using the method described above. Using this conclusion, we will now relate the number of sides of a polygon, the number of triangles that can be formed by drawing diagonals and the polygon’s angle sum.

table

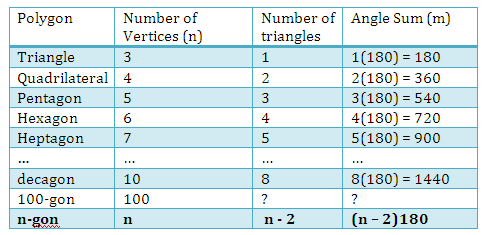
From the table above, we observe that the number of triangles formed is $2$ less than the number of sides of the polygon. This is true, because $n - 2$ triangles can be formed by drawing diagonals from one of the vertices to $n - 3$ non-adjacent vertices. Therefore, there the angle sum $m$ of a polygon with $n$ sides is given by the formula

$m = 180(n - 2)$

A More Formal Proof

Theorem: The sum of the interior angles of a polygon with $n$ sides is $180(n-2)$ degrees.

Proof:

Assume a polygon has $n$ sides. Choose an arbitrary vertex, say vertex $V$ . Then there are $n - 3$ non-adjacent vertices to vertex $V$ . If diagonals are drawn from vertex $V$ to all non-adjacent vertices, then $n - 2$ triangles will be formed. The sum the interior angles of $n -2$ triangles is $180(n - 2)$ . Since the angle sum of the polygon with $n$ sides is equal to the sum the interior angles of $n - 2$ triangles, the angle sum of a polygon with $n$ sides is $180(n-2)$ . $\blacksquare$

Exercises:

1.) Find the number the angle sum of a dodecagon ( $12$ -sided polygon).

2.) The angle sum of a polygon is $3240$ degrees. What is the number of its sides?

3.) The measure of one of the angles of a regular polygon is $150$ . Find its number of sides.

4.) From this, prove that the sum of the interior angles of a polygon is $360$ degrees.

5 comments angle sum, angle sum maths, angle sum of a pentagon, angle sum of a triangle, angle sum of polygons, angle sum of quadrilatearl, geometry angle sum, sum of interior angles of a polygon

Why do we reverse/flip the inequality sign?

October 15, 2009 GB High School Algebra, High School Mathematics, Questions and Quandaries

You have probably remembered in Algebra that if we multiply an inequality by a negative number, then the inequality sign should be flipped or reversed. For example, if we want to find the solution of the inequality $-\frac{1}{2}x > 8$ , we multiply both sides by $-2$ and reverse the greater than sign giving us $x < -16$ . Now, why did the $>$ sign became $<$ ?

If we generalize the statements above, suppose we have two numbers, say, $a$ and $b$ such that $a > b$ , if we multiply them to a negative number $c$ , instead of having $ac > bc$ , the answer should be $ac < bc$ .

Before we proceed with our discussion, let us first remember 2 basic concepts we have learned in elementary mathematics:

The number line is arranged in such a way that the negative numbers are at the left hand side of $0$ and the positive numbers are at its right hand side such as shown in Figure 1.
If we have $2$ numbers $a$ and $b$ , then $a > b$ if $a$ is at the right of $b$ on the number line. For example, in Figure 1, $2 > -1$ since $2$ is at the right of $-1$ .

Figure 1 – The number line

For specific values, let’s choose $a = 2$ and $b = -1$ as shown in the diagram above and choose $c = -1$ . Note that we will just use these values for discussion purposes, but we may take any values. It would help, if we think of $a$ and $b$ as two points on the number line with $a$ as a blue point on the right $b$ , a red point.

And note that before multiplying with a negative number, VALUE OF BLUE POINT > VALUE OF RED POINT.

Since $a$ and $b$ are variables, we need to multiply all the numbers on the number line by $-1$ . This is to ensure that whatever values we choose for $a$ and $b$ , we multiply them by $-1$ . If we multiply every number on the number line by $-1$ , the geometric consequence would be a number line with negative numbers on the right hand side of $0$ , and positive numbers at the left hand side of $0$ as shown in Figure 2.

Figure 2 – Afer multiplying all numbers on the number line by -1

But negative numbers should be at the left hand side of $0$ so we reverse its position by rotating it 180 degrees from any point of rotation (for example, 0). The resulting figure is shown in Figure 3.

Figure 2 - All numbers in the number line were multiplied by -1

Notice that the blue and red points changed order and that the blue point is now at the left of the red point. Therefore, VALUE OF BLUE POINT < VALUE OF RED POINT. That is, why the inequality sign was reversed.

Summarizing, multiplying an inequality by a negative number is the same as reversing their order on the number line. That is, if $a, b$ and $c$ are real numbers, $a > b$ and $c<0$ , then $ac < bc$ .

Our summary above is actually a mathematical theorem. The proof of this is shown below. It is a very easy proof, so, I suppose, that you would be able to understand it.

Theorem: If $a, b$ and $c$ are real numbers, with $a > b$ and $c<0$ , then $ac < bc$ .

Proof:

Subtracting $b$ from both sides, we have $a - b>0$ .

Now, $a - b>0$ means $a - b$ is positive.

Since $c$ is negative, therefore, $c(a - b)$ is negative (negative multiplied by positive is negative)

Since $c(a - b)$ is negative, therefore, $c(a - b) < 0$ .

Distributing $c$ , we have $ac - bc < 0$ .

Adding $bc$ to both sides, we have $ac < bc$ which is what we want to show . $\blacksquare$

Leave a comment flip inequality sign, flip inequality sign dividing negative, inequality sign change, switch the inequality sign, when do you flip inequality sign

Problem Set 2

October 13, 2009 GB Problems Sets

PROBLEMS

1.) Find a linear function $f(x)$ such that $f(1) = 42$ and $f(2) = 47$ .

2.) Solve for $x$ : $4^{x+1} + 4^{x+2} +4^{x+3} +4^{x+4} = 170.$

3.) Prove that the product of $3$ consecutive numbers is always divisible by $6$ .

4.) Prove that if $p$ is prime, $a$ and $b$ are integers, and $a \equiv b\mod p$ , then $a^p \equiv b^p \mod p$ .

SOLUTIONS AND PROOFS

Post Date: October 20, 2009

1. Solution: This is just the same as saying, find the equation of the line passing through $(1,42)$ and $(2,1337)$ . So, by point slope formula, we have, $y - y_1 = \displaystyle\frac{y_2 - y_1}{x_2 - x_1}(x - x_1)\Rightarrow y - 42 = \displaystyle\frac{1337 - 42}{2 - 1}(x - 1). \Rightarrow y = f(x) = -18x + 92.$

2.) Solution: $4^{x+1} + 4^{x+2} +4^{x+3} +4^{x+4} = 4^x(1 + 4 +4^2 +4^3) = 170 \Rightarrow 4^x(85) = 170\Rightarrow 4^x = 2 \Rightarrow 2^{2x}=2^1 \Rightarrow x = \displaystyle\frac{1}{2}.$

3.) Proof: A number is divisible by $6$ if it is divisible by $2$ and $3$ . A product of $3$ consecutive numbers is divisible by $2$ because at least one of them is even, so it remains to show it is divisible by $3$ .

If a number is divided by $3$ , its possible remainders are $0, 1,$ and $2$ . Assume $n, n +1$ and $n+2$ be the three consecutive numbers, and $r$ be the remainder if $n$ is divided by $3$ .

Case 1: If $r=0$ , we are done.

Case 2: If $r = 1$ , then $n + 2 \Rightarrow r=0$

Case 3: If $r = 2$ , then $n + 1 \Rightarrow r = 0$ .

Since the product of the three consecutive numbers is even, and for each case of $r$ , one of the consecutive numbers is divisible by $3$ , the product of three consecutive numbers is divisible by $6. \blacksquare$

4.) Proof: From definition, $a^p \equiv b^p \mod p \Leftrightarrow b = a + kp$ for some $k \in \mathbb{Z}.$

Raising both sides of the equation to $p$ , we have $b^p = (a + kp)^p.$ By the binomial theorem, $b^p = (a + kp)^p = a^p + \displaystyle {p \choose 1}a^{p-1}kp + \displaystyle{p \choose 2}a^{p-2}k^2p^2 + \ldots + k^pp^p$ .