Pythagorean Theorem, Distance Formula, and Equation of a Circle

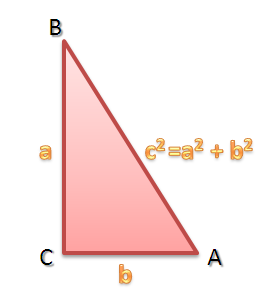
In my Algebraic and Geometric Proof of the Pythagorean Theorem post, we have learned that a right triangle with side lengths $a$ and $b$ and hypotenuse length $c$ , the sum of the squares of $a$ and $b$ is equal to the square of $c$ . Placing it in equation form we have $c^2 = a^2 + b^2$ .

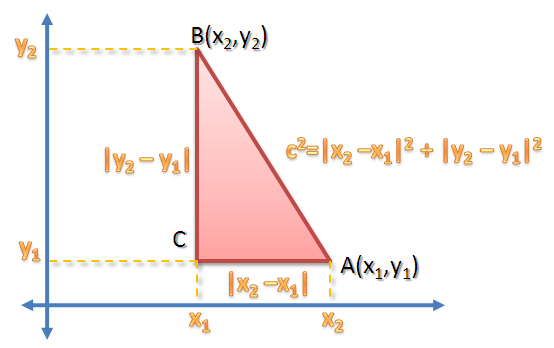
If we place the triangle in the coordinate plane, having $A$ and $B$ coordinates of $(x_1,y_1)$ and $(x_2,y_2)$ respectively, it is clear that the length of $AC$ is $|x_2 - x_1|$ and the length of $BC$ is $|x_2 - x_1|$ . We are finding the length, which means that we want a positive value; the absolute value signs guarantee that the result of the operation is always positive. But in the final equation, $c^2 = |x_2 - x_1|^2 + |y_2-y_1|^2$ , the absolute value sign is not needed since we squared all the terms, and squared numbers are always positive. Getting the square root of both sides we have,

$c = \sqrt{|x_2 - x_1|^2 + |y_2-y_1|^2}$

We say that $c$ is the distance between $A$ and $B$ , and we call the formula above, the distance formula.

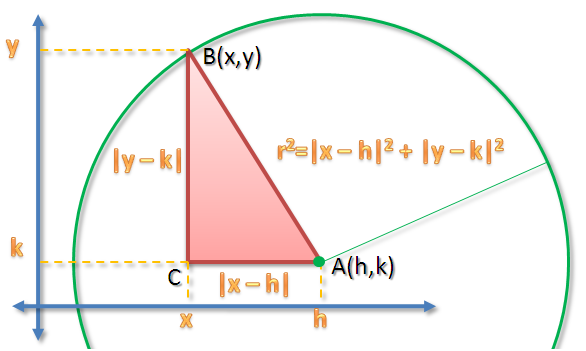
If we want coordinates of $B(x,y)$ where $x$ and $y$ are variables and the distance of $B$ from $A$ constant, say $r$ , then moving point $B$ about point $D$ maintaining the distance $r$ forms a circle. If $A$ has coordinates $(h,k)$ , then $r^2 = (x-h)^2 + (y-k)^2$ which means that $r = \sqrt{ x-h)^2 + (y-k)^2}$ .

Observe that the two equations above are all of the same form, they are all consequences of the Pythagorean Theorem. The examples are probably very elementary, but it shows one of the rare beauties of mathematics — the strong connections between and among different concepts.