hypotenuse of a right triangle Archives

Pythagorean Theorem, Distance Formula, and Equation of a Circle

July 19, 2010 GB High School Geometry, High School Mathematics

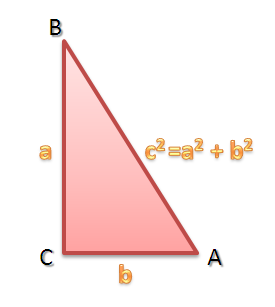
In my Algebraic and Geometric Proof of the Pythagorean Theorem post, we have learned that a right triangle with side lengths $a$ and $b$ and hypotenuse length $c$ , the sum of the squares of $a$ and $b$ is equal to the square of $c$ . Placing it in equation form we have $c^2 = a^2 + b^2$ .

If we place the triangle in the coordinate plane, having $A$ and $B$ coordinates of $(x_1,y_1)$ and $(x_2,y_2)$ respectively, it is clear that the length of $AC$ is $|x_2 - x_1|$ and the length of $BC$ is $|x_2 - x_1|$ . We are finding the length, which means that we want a positive value; the absolute value signs guarantee that the result of the operation is always positive. But in the final equation, $c^2 = |x_2 - x_1|^2 + |y_2-y_1|^2$ , the absolute value sign is not needed since we squared all the terms, and squared numbers are always positive. Getting the square root of both sides we have,