Introduction
If we want to find the midpoint of segment CD in Figure 1, where the coordinates of points C and D are 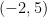 and
and  , it is clear that the length of CD is
, it is clear that the length of CD is  units. To determine the midpoint of CD, we want to get the coordinates of the point which is
units. To determine the midpoint of CD, we want to get the coordinates of the point which is 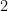 units away from both points C and D. Hence, we have to divide
units away from both points C and D. Hence, we have to divide  by
by 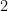 , and add the result to
, and add the result to 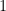 or subtract the result from
or subtract the result from 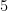 . Summarizing, the expression that would describe the value of the y-coordinate of the midpoint would be
. Summarizing, the expression that would describe the value of the y-coordinate of the midpoint would be 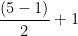 or
or  . This means that the midpoint of CD is
. This means that the midpoint of CD is  .
.
If we want to get the midpoint of AB, using the same reasoning above, the expression that would describe the x-coordinate of the midpoint would be 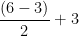 or
or  . This means that the midpoint of AB is
. This means that the midpoint of AB is 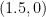 .
.
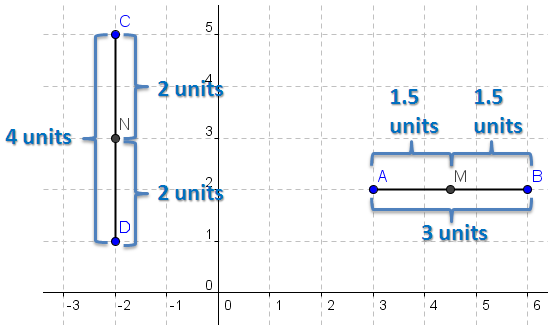
Figure 1 – Horizontal line AB and vertical line CD in the coordinate plane.
Generalizing our observation above, if we have a vertical segment with their endpoints having coordinates 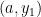 and
and 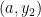 (see Figure 2), we can get its midpoint using the following formula
(see Figure 2), we can get its midpoint using the following formula  or
or 
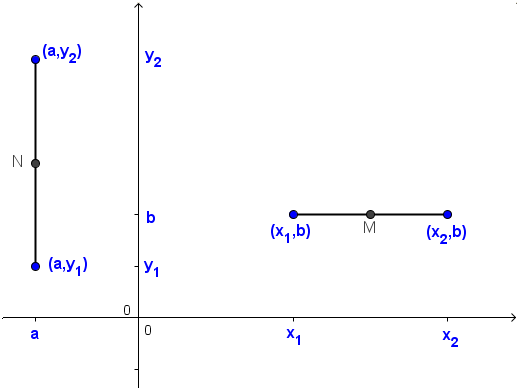
Figure 2 – Generalized coordinates of a vertical and a horizontal line.
Simplifying, both the expressions above result to  . Similarly, for a horizontal segment with endpoints having coordinates
. Similarly, for a horizontal segment with endpoints having coordinates  and
and  can be computed by the expression
can be computed by the expression  .
.
Midpoint of a Slanting Segment
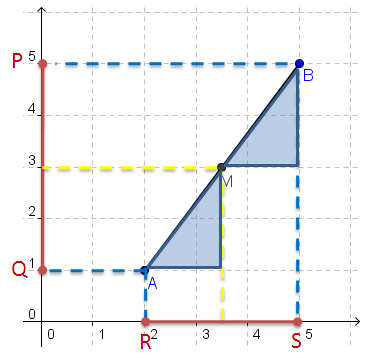
The preceding derivations are only valid for vertical and horizontal segments. In Figure 3, segment AB is neither horizontal nor vertical. To investigate the midpoint of AB, we draw vertical segment PQ coinciding with the y-axis with endpoints having y-coordinates the same as those of the y-coordinates of segment AB (see Figure 3). We also draw a horizontal line RS coinciding the x-axis with endpoints having x-coordinates the same as those of the x-coordinates of segment AB. Looking at Figure 3, it is clear that the coordinates of the midpoint of the PQ is  .
.
If we draw a horizontal line from  towards segment AB (see yellow dashed segment), and draw a vertical line from the intersection M to segment RS, it seems that the intersection of the yellow dashed line and segment RS is
towards segment AB (see yellow dashed segment), and draw a vertical line from the intersection M to segment RS, it seems that the intersection of the yellow dashed line and segment RS is 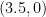 which is the midpoint of RS. From here, it is tempting to ask the following question:
which is the midpoint of RS. From here, it is tempting to ask the following question:
“If the midpoint of PQ is 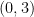 and the midpoint of RS is
and the midpoint of RS is 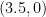 , is the midpoint of AB,
, is the midpoint of AB,  ?
?

Figure 3 – A non-horizontal segment AB with midpoint M.
Generalizing the questions above, we might want to ask “If the midpoint the point with coordinates A 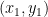 and B
and B 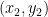 equal to
equal to  ?”
?”
If we extend the QA and the horizontal yellow dashed line to the right, we can from two right triangles as shown in Figure 4. From the statements above, we want to show that point M is the midpoint of AB.
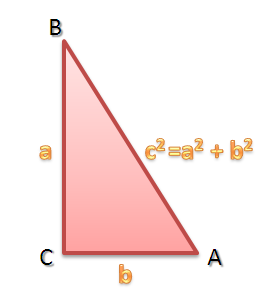
To show that M is the midpoint of AB, it is sufficient to show that AM is congruent to MB. This leads us to Figure 5, where we label the right angles of the two triangles T and U. We will now show that triangle AUM is congruent to triangle MTB. If so, then we can show that AM is congruent to MB since they are the corresponding sides of the given triangles.
Proof that AUM is congruent to MTB
Since PB and MT are horizontal segments, we can consider AB as a transversal of parallel segments PB and the segment containing MT. It follows that angle TBM and angle UMA are congruent because they are corresponding angles. It is also clear that BT is congruent to MU, and angle T is congruent to angle U since they are both right angles. Therefore, by the ASA congruence theorem, AUM is congruent to MTB. (For an explanation of parallel lines and transversals, click here).
Since corresponding parts of congruent triangles are congruent, AM is congruent to MB. Hence, M is the midpoint of AB.

Figure 5 – The triangle produced by extending the horizontal lines passing through the three points.
Note that our proof did not talk about coordinates, but the general case. That is, if the coordinates of A are  and the coordinates of B are
and the coordinates of B are 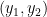 , the coordinates of M is equal to
, the coordinates of M is equal to 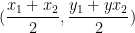 .
.
Delving Deeper
There are also other ways to show that the midpoint of AB is M.  and
and  lies on the midpoint formula. The details of the solutions are left to the reader as an exercise.
lies on the midpoint formula. The details of the solutions are left to the reader as an exercise.
- From Figure 3, draw two right triangles with hypotenuse AM and hypotenuse AB and show that AM is half of AB.
- Using the distance formula, show that the distance between point A and point M is the same as the distance between point M and point B.
- Show that AM and MB has the same slope.
- Get the equation of the line containing AB, and substitute the coordinates of M to the equation of line AB.