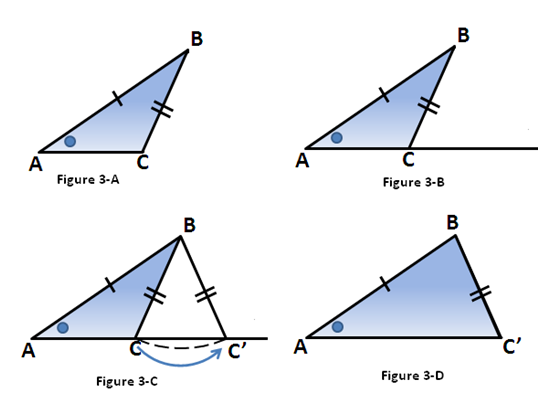
Geometer’s Sketchpad Essentials 4 – The SSS Triangle Congruence
This is the fourth part of the Geometer’s Sketchpad Essentials Series. In this tutorial, we are going to construct another triangle which is congruent to a given triangle using the concept of the SSS triangle congruence. Recall that the SSS congruence theorem tells us that two triangles are congruent, if their corresponding sides are congruent. In doing the construction, we are going to learn how to use the Ray tool, the Circle tool, and other commands.
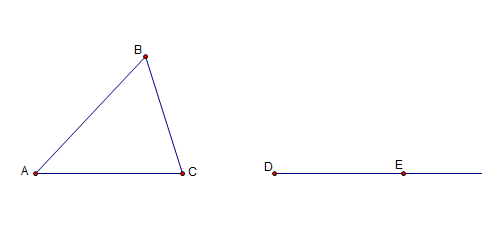
1.) Construct triangle ABC.
2.) Next, we construct ray DE. To do this, click the Straightedge tool box and hold the mouse button to display the other tools. Now, choose the Ray tool.
3.) Click two distinct points on the sketch pad and display the names of the two points. Your sketch should look like the first figure.
 4.) Next, we will construct a segment DF which is congruent to AC. To do this, be sure to deselect all the objects by clicking on the vacant part of the sketch pad. Select point D, then select segment AC (do not select the points!), click the Construct menu, and then click Circle By Center+Radius. This will produce a circle with center D and radius equal to the length of AC. » Read more
4.) Next, we will construct a segment DF which is congruent to AC. To do this, be sure to deselect all the objects by clicking on the vacant part of the sketch pad. Select point D, then select segment AC (do not select the points!), click the Construct menu, and then click Circle By Center+Radius. This will produce a circle with center D and radius equal to the length of AC. » Read more