GeoGebra Essentials 3 – Triangles, Incircles, and Circumcircles
This is the third tutorial in the GeoGebra Essentials Series. If you are entirely new to GeoGebra, you should read the Introduction to GeoGebra post and prior tutorials. It contains the pre-requisites of this tutorial.
In the tutorial below, menu commands, located in the menu bar, are in brown bold text, and submenus are denoted by the > symbol. For example, Options>Labeling> New Points Only means, click the Options menu, choose Labeling from the list, then select New Points Only. The GeoGebra tools are denoted by orange bold texts. For example, New Point means the new point tool.
In this tutorial, we show that in any triangle, we can always create a circle passing through its three vertices, and we can always create an inscribed circle. The circle that passes through the three vertices of a triangle is called the circumcircle of the triangle, while the inscribed circle is called its incircle.
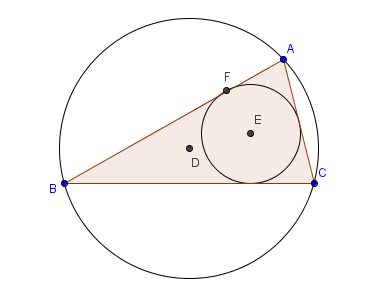
To create the circumcircle of triangle ABC, we find the intersection of the perpendicular bisectors of its three sides. The intersection, known as the circumcenter, will be the center of the circumcircle. To construct the incircle, we find the intersection of the three angle bisectors of its interior angles. The intersection, known as the incenter, will be the center of the incircle.
In doing the tutorial, we learn the following:
- Use the tools we have discussed in GeoGebra Essentials 1 and GeoGebra Essentials 2
- Learn how to use new tools including Polygon, Perpendicular Bisector, Angle Bisector, and Delete
| 1.) Open GeoGebra. Select Geometry from the Perspective panel at the Sidebar to remove the axes and the Algebra view. Label the new points only by selecting Options>Labeling> New Points Only from the menu bar. | |
| 2.) Select the Polygon tool, click on three different locations on the Graphics view to construct triangle ABC, and then click on point A to close the polygon. | |
| 3.) We construct perpendicular bisectors of the three sides of the triangle. To construct the perpendicular bisector of AB, select the Perpendicular Bisector tool, and then click on side AB1. Next, construct the perpendicular bisectors of AC and BC. | |
| 4.) Now, select the Move tool and drag the vertices of the triangle. What do you observe? What conjecture can you make from your observation? | |
5.) Select the Intersect tool, and then click on the intersection of the three lines to produce point D.
 Figure 1 |
|
| 6.) Point D is the center of the circle passing through the three vertices of the triangle. So, to construct the circumcircle, select the Circle with Center through Point, click point D, and then click on point A2. | |
| 7.) Drag the vertices of the triangle. What do you observe? We now hide all the lines. Right click each of the lines and then click Show Object to hide it. | |
8.) We now construct the inscribed circle. To construct the angle bisector of angle A, select the Angle Bisector tool, click on point B, click on point A and then click on point C. Now construct the angle bisectors of angles B and C.
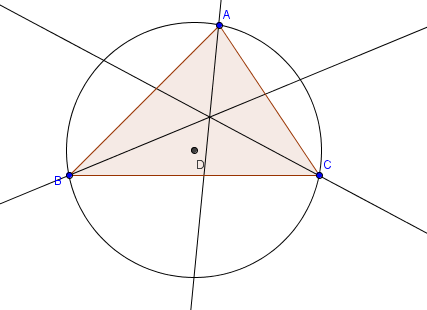 Figure 2 |
|
|
|
9.) Intersect the bisectors by selecting the Intersect tool and then selecting any of the two angle bisectors. This will produce point E. Repeat step 7 and, again, hide the three lines. |
|
|
10. Point E is the center of the inscribed circle. We now construct a line perpendicular to AB and passing through E3. To do this, select the Perpendicular Line tool, click point E and then click segment AB (click the segment, not the endpoints). |
|
|
11. Using the Intersect tool, intersect segment AB and the line perpendicular to it. This will produce point F as shown in Figure 3.
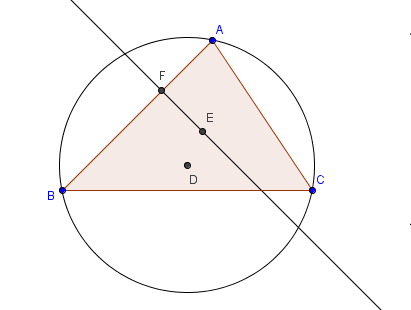 Figure 3 |
|
|
12. To construct the inscribed circle, select the Circle with Center through Point,click point E and then click point F.Repeat step 7 and hide the line. |
| 13. Save your file by clicking File>Save on the menu bar. Name your file as essentials3. |
Notes:
1Click the segments and click not the endpoints. Another way to contruct a perpendicular bisector is to click the Perpendicular Bisector tool and then click the endpoints.
2Of course, you can click any of the two vertices, not just point A.
3This is because the line tangent to a circle is perpendicular to the radius at the point of tangency F.
Last Update: 20 October 2015 (GeoGebra 5.0)