This is the third tutorial in the GeoGebra Essentials Series. If you are entirely new to GeoGebra, you should read the Introduction to GeoGebra post and prior tutorials. It contains the pre-requisites of this tutorial.
In the tutorial below, menu commands, located in the menu bar, are in brown bold text, and submenus are denoted by the > symbol. For example, Options>Labeling> New Points Only means, click the Options menu, choose Labeling from the list, then select New Points Only. The GeoGebra tools are denoted by orange bold texts. For example, New Point means the new point tool.
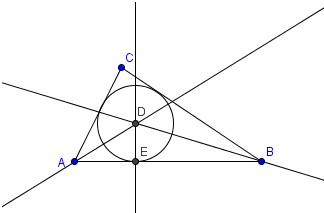
In this tutorial, we show that in any triangle, we can always create a circle passing through its three vertices, and we can always create an inscribed circle. The circle that passes through the three vertices of a triangle is called the circumcircle of the triangle, while the inscribed circle is called its incircle.
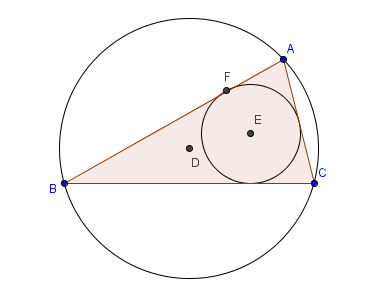
To create the circumcircle of triangle ABC, we find the intersection of the perpendicular bisectors of its three sides. The intersection, known as the circumcenter, will be the center of the circumcircle. To construct the incircle, we find the intersection of the three angle bisectors of its interior angles. The intersection, known as the incenter, will be the center of the incircle. » Read more