Experimental and Theoretical Probability 5

This is the fifth and the final part of the Experimental and Theoretical Probability Series.  In this post, we are going to summarize what we have discussed in the previous four posts, and we are going to talk about some  real-life applications of experimental and theoretical probability.

Experimental Probability, as we have discussed in the fourth part of this series, may be obtained by conducting experiments and recording the results. It is the ratio of the number of times an  event occurs to the total number of trials. In the first part of this series, we experimented rolling to dice 1000 times (via a spreadsheet) and we tallied the sums.  We recorded the that sum 2 occurred 29 times out of 1000 trials. We can say that the experimental probability of getting a 2 from that particular experiment is 29/1000.

We also confirmed  that some sums such as 6, 7, 8 occured more frequently than the others, and in third part of the series, we have discoverd why.  By listing all the sums and all the ways they could be obtained, we have discovered that there are more ways to obtain sums like 6, 7, and 8 than 1 or 12.  We have discovered that there is only one way to get a sum of 2; that is, 1 and 1 and there are 36 ways of getting all the possible sums. We can say that the theoretical probability of getting a 2 in rolling two standard cubical dice is 1/36.  As we have discussed in the fourth part of this series, theoretical probability of an event is the number of favorable outcomes over the total number of possible outcomes.

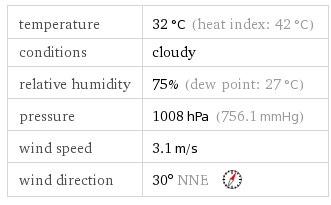
In real life, experimental probability is done in many scientific research. For example, we are able to predict the weather by recognizing patterns from data that had been collected over the years.

The table below shows the weather data in our country the time I began writing this (according to Wolfram Alpha). If we have, say, 30,000 days recorded in our weather database, and 2000 days, has the same data as above (including other data), and out of the 2000 days, 500 days rained heavily, then it is safe to conclude that there is 500/2000 or  25% probability that it will rain heavilty today. Of course, the more data we have collected, the more accurate our prediction.

Theoretical probability, on the other hand, is used more to make decisions that will be favorable to certain choices.  In casinos, for instance, mathematicians designed each game that would be favorable to the house (casinos). This means that even if a casino does not cheat (hopefully), if you continue playing, you will definitely lose.

For example, a casino may design a die game where the banker throws a die and each player choose a number. The casino will not design and odd-even game (odd: player wins; even: casino wins) because it’s an even game. A casino might choose the following condition:

If the sums of two dice are 5,6,7,8,9: casino wins, other wise, player wins. Now, the players will think that they will win because they have 6 sums to chose from (1, 2, 3, 10, 11, 12) and the casino has only five, but the truth is, the probability of the casino winning is 24/36, while the player has only 12/36 (can you see why?). That means, in three games, it is more likely, that the the casino will win twice.