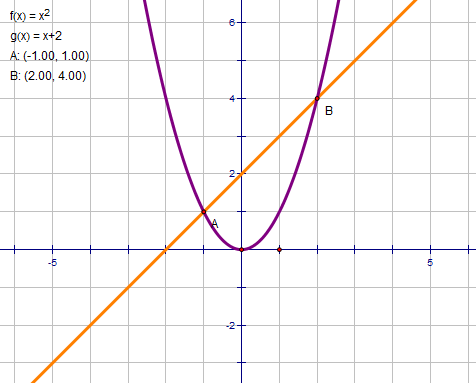
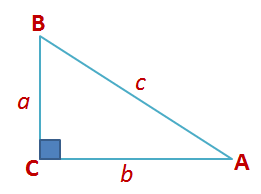
September 2011 Week 1 Posts Summary
Mathematics and Multimedia
- The Kaprekar Constant 6174
- Math and Multimedia Carnival 14
- Guest Posting Guidelines
- Create Flipbooks with Youblisher
- The Complements Theorem
- Geometer’s Sketchpad Essentials 5 – Basic Graphing
- Napeleon’s Theorem and Constructing and Equilateral Triangle from GeoGebra Applet Central
- Blog appearance, design, and structure tips (part 1 and part 2) from Blogineering
- Creating Online Notes with Pen.io at Freebie School