The need of men to perform certain mathematical operations led to the birth of different types of numbers. People in the ancient times used only counting numbers to keep track of the number of their belongings such as animals. The concept of trade led to the invention of 0 and negative numbers. The need to divide led to the invention of rational numbers.
In this article, we are going to take a look at the characteristics of rational and irrational numbers.
Rational numbers are numbers of the form a/b where a, b are integers, and b not equal to zero. Rational numbers are called rational not because they are reasonable, but because they are a ratio of two integers. It is worthy to note the conditions in the definition. That is because not all fractions are rational numbers. For example,  is a fraction, but it is only a rational number when simplified. From the definition, we can deduce that all integers are rational numbers since {…,-3, -2, -1, 0, 1, 2, 3,…} = {…, -3/1, -2/1, -1/1, 0/1, 2/1, 3/1, …}.
is a fraction, but it is only a rational number when simplified. From the definition, we can deduce that all integers are rational numbers since {…,-3, -2, -1, 0, 1, 2, 3,…} = {…, -3/1, -2/1, -1/1, 0/1, 2/1, 3/1, …}.
Geometric Interpretation of Rational and Irrational Numbers
In ancient times the Greeks, particularly the Pythagoreans, believed that all quantities are rational; that is, all quantities can be expressed as a ratio of two integers. Geometrically, this can be interpreted as follows. Given any two lengths, a unit length can be found that can measure the two lengths exactly without gaps or overlaps. In the example in Figure 1, we have two segments a and b, and we found a unit length that would fit exactly a whole number of times in both segments. The ratio of a:b is 7:6, or we can express it in a fraction that a is 7/6th of b.
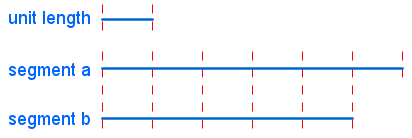
Figure 1 – The division of segments a and b into unit lengths.
This belief, as most of us now know, was proven to be false. The Pythagoreans later discovered that given a square with length 1 unit, no unit length, however short, can be found to measure both the side of the square and its diagonal like what we have done above. They have concluded that the length of the diagonal cannot be expressed as the ratio of two integers and hence not rational. Today, numbers that are not rational are called irrational numbers. Hence, we define irrational numbers as numbers that cannot be expressed as a ratio of two integers.

Figure 2 – The square with length 1 unit has irrational diagonal.
Using the Pythagorean Theorem, we now know that the length of the diagonal of a square with side length 1 unit is equal to 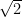 . We have already discussed and proved that
. We have already discussed and proved that  is irrational.
is irrational.
The collection of all rational and irrational numbers is called real numbers. Geometrically, real numbers are represented by the real line as shown in Figure 3.
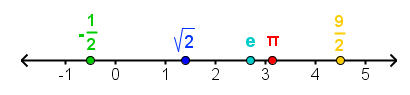
Figure 3 – The real number line.
Each real number can be represented by a point on the real number line and every point on the number line has a corresponding real number.
Another Representation of Rational and Irrational Numbers
Aside from fractions, we can also represent rational numbers with decimals. For example, 1/5 = 0.2 and 1/3 = 0.333…. Observe that 0.2 has a finite number of decimals while 0.333… has infinite. Irrational numbers can also be represented using decimals. They are the types of decimals that do not end and do not repeat.
Several irrational numbers are very popular, and we had been using them from elementary school to college. The irrational numbers 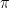 ,
,  and
and 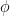 are several of irrational numbers that we are acquainted with.
are several of irrational numbers that we are acquainted with.
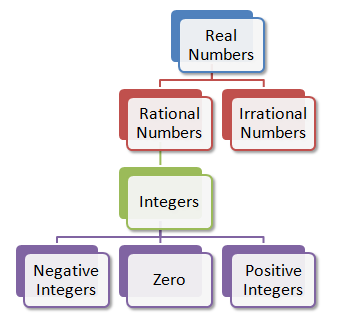
Figure 4 – The structure of the real number system.
From our discussion above, we can see that real numbers are divided into two main subsets – rational and irrational numbers.





