In the Understanding the Fermat’s Last Theorem post, I have mentioned about Pythagorean Triples. In this post, we will show that there are infinitely many of them. We will use intuitive reasoning to prove the theorem.
For the 100th time (kidding), recall that the Pythagorean Theorem states that in a right triangle with side lengths 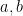 and
and  , where
, where  is the hypotenuse, the equation
is the hypotenuse, the equation 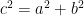 is satisfied. For example, if we have a triangle with side lengths
is satisfied. For example, if we have a triangle with side lengths 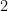 and
and 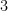 units, then the hypotenuse is
units, then the hypotenuse is 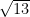 . The converse of the Pythagorean theorem is also true: If you have side lengths,
. The converse of the Pythagorean theorem is also true: If you have side lengths, 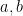 and
and  , which satisfies the equation above, we are sure that the angle opposite to the longest side is a right angle.
, which satisfies the equation above, we are sure that the angle opposite to the longest side is a right angle.
We are familiar with right triangles with integral sides. The triangle with sides 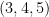 units, for instance, is a right triangle. This is also the same with
units, for instance, is a right triangle. This is also the same with  and
and  . We will call this triples, the Pythagorean triples ,or geometrically, right triangles having integral side lengths. » Read more
. We will call this triples, the Pythagorean triples ,or geometrically, right triangles having integral side lengths. » Read more
