compass and ruler software Archives

CaR Tutorial 2 – The MidSegment Theorem

March 3, 2010 GB Compass and Ruler, High School Geometry, Software Tutorials

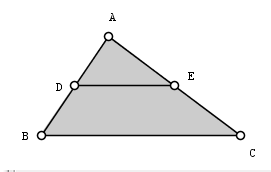
In the previous CaR tutorial, we constructed and isosceles triangle. In this tutorial we are going to explore the properties of the segment connecting the midpoints of its two sides. In this tutorial we are going to learn the following:

use the move tool, triangle tool and segment tool
find the midpoint of two a segment
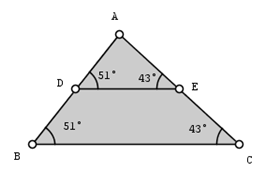
measure angles using the angle tool
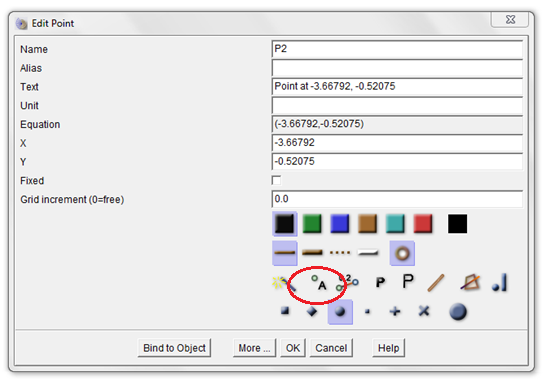
edit properties and reveal measures of angles and segments

Construction Steps

	1.) Open CaR. We will not need the Coordinate axes so click the Show grid icon until the Show the Grid icon until the grid or axes is not shown.
	2.) Click the Triangle tool and click three different points on the drawing pad.
	3.) Click the Move tool and right click one of the points to display the Edit Point dialog box. In the Name text box, change the name to A, then click the Show object names button (enclosed with red ellipse in Figure 1). Figure 1 – The Edit Point dialog box.
	4.) Change the name of the other two points to B and C.
	5.) Click the midpoint tool, click point A and click point B to get the midpoint of AB. Now, get the midpoint of BC. Rename the midpoint of AB to E and the midpoint of AC to F (Refer to step 3). Your drawing should look like Figure 2. Figure 2 – Triangle ABC with midpoints D and E.
	6.) Right click and drag the labels to adjust their positions. Using the Move tool, move the vertices of the triangle. What do you observe?
	7.) We will see the relationship of the angles and the segments in triangle ABC. We will measure the angle first. To measure angle ADE, click the points in the following order: point A, point B and point C. After this step, you will see the angle symbol at angle *ADE*.
	8.) To display the measure of the angle, click the Move tool and right click the angle symbol. This will display the Edit Angle dialog box shown in Figure 2.
	9.) To display the measure of the angle, click the Show object values icon. Then click the smallest angle symbol size to reduce the angle size. Now, click the OK button to apply changes. Figure 3 – The Edit Angle dialog box.
	10.) Using step 8-9, measure angles *ABC, ACB* and *AED*. After measuring, your drawing should look like the figure below.
	11.) Using the Move tool, drag the vertices of the triangle. What do you observe?
	12.) Based on the measures of the angles shown in your drawing, what can you say about segment DE and segment BC?
	13. ) Now, we will see if there is a relationship between the length of the segments in triangle *ABC. To reveal the measure of DE, use the Move tool* and right click the segment. This will reveal the Edit Line, Ray, Segment dialog box as shown in Figure 3. Figure 5 - The Edit Line, Ray, Segment dialog box.
	14.) In the Edit Line, Ray, Segment dialog box, click the Show object values button.
	15.) Using steps 13-14, display the length of segment BC.
	16.) What can you observe about the relationship of segments DE and BC?
	17.) Move the vertices of the triangle. Are your observations still the same?
	18.) Make a conjecture about your observations above.

One comment compass and ruler software, dynamic geometry, free, free math software, free software, midline theorem, midpoint of sides of a triangle

CaR Tutorial 1- Constructing an Isosceles Triangle

February 22, 2010 GB Compass and Ruler, Software Tutorials

CaR or Compass and Ruler is a free dynamic geometry software written in Java by Rene Grothman. The CaR window is shown below.

Figure 1 - The Compass and Ruler window.

The upper part of the window contains the menu bar and toolbar. The toolbar contain tools in constructing and editing mathematical objects. The left window below the toolbar is the Objects window and the right pane is the Drawing pad where we construct drawings.

Tutorial 1 – Constructing an Isosceles Triangle

In the first tutorial, we are going to create an isosceles triangle by using the center of the circle and two points on its circumference.

	1.) We will not need the Coordinate axes so click the Show grid icon until the Show the Grid icon until the grid or axes is not shown.
	2.)Click the Circle tool, then click the drawing pad to determine the center of the circle, and click another location to determine its radius.
	3.) Click the Point tool and click another location on the circumference circle. After step 3, your drawing should look like the figure below. Figure 2 - Circle with 2 points on its circumference.
	4.) Click the Segment tool and two points to construct a side of the triangle. Continue until the triangle is formed.
	5.) Click the Move button to drag the points and observe what happens to the triangle. Explain why the triangle is always isosceles.
	6.) Click the Hide object button and click the circle to hide it.
	7.) Next, we will change the name of the points and display their names. To do this, right click a point to display the Edit Point dialog box. In the Name text box, type A, then click the Show Object Names icon. Figure 1 - The Edit Point Dialog box. Use the same process to change the name of the other points.