Tag: midline theorem

Wingeom Tutorial 1 – The Midline Theorem

Software Tutorials, Web 2.0 Technology, Wingeom

Introduction

Wingeom is a dynamic geometry software created by Philip Exeter University.  It is capable of 2-dimensional and 3-dimensional geometric drawing and construction.

This is the first tutorial of the Wingeom Tutorial Series.  Most of the construction in this tutorial series will deal with 2-dimensions.

The Wingeom Environment

When you open Wingeom, the window shown below will appear. You have to click the Window menu, then choose the environment that you want to display.  Wingeom can construct figures in Euclidean, hyperoblic and spherical plane.

Figure 1 – The Wingeom window.

It is also capable of constructing Voronoi diagrams and tessellations.

Using Wingeom in Exploring the Midline Theorem

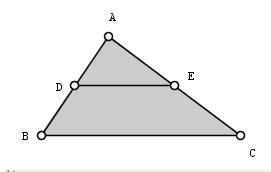
In this construction, we will explore the relationship of a triangle and its midline (or midsegment), the segment connecting the midpoints of its two sides as shown in Figure 2.

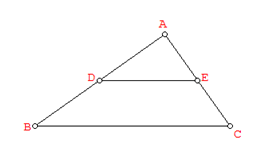
Figure 2 – Triangle ABC with midline DE.

In the construction below, we will construct 3 points A, B and C and connect them with the segment tool. After drawing the triangle, we will get the midpoints of AB and AC and explore the length and interior angles of the two triangles formed.

To perform the construction, follow the construction steps below and answer the questions.

Construction Steps

1.)    To open the construction window shown in Figure 2, click the Window menu and then click the 2-dim option.

2.)    Next we will show the Wingeom toolbar. The toolbar displays the tool that we can use to draw and manipulate geometric figures.  To display the toolbar, click the Btns menu and then click Toolbar.

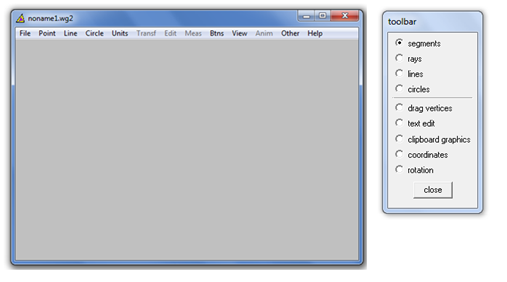
Figure 3 – The Wingeom window and its toolbar.

3.)  The first step in our construction, we will draw the vertices of our triangle. To do this, right click three different locations on the drawing pad. Notice that Wingeom automatically names the points in alphabetical order.

4.)    Next, to construct the sides of the triangle, select the segments option button in the toolbar then drag point A to point B to construct segment AB.

5.)    Using the steps in 4, draw segments AC and BC.

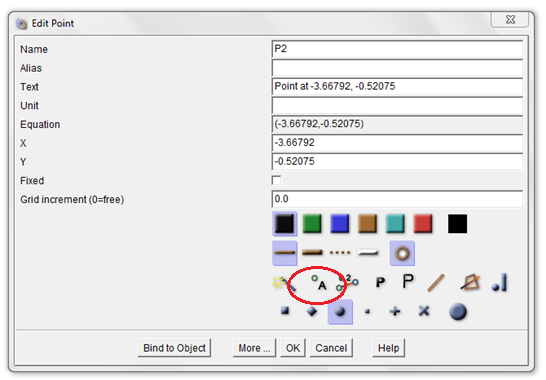
6.)    Next, we will draw the midpoint of AB. To do this, click the Point menu and then click on Segment… to display the new point dialog box.

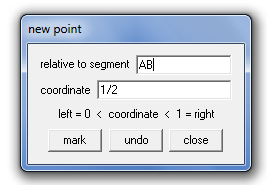
Figure 4 – The new point dialog box.

7.)    In the relative to segment, type AB, leave the coordinate to 1/2 and then click the mark button. Notice that point now lies on AB. This means that Wingeom should construct a segment halfway of AB.

8.)     To create a midpoint of AC, delete the text in the relative to segment text box and type AC. Then click the mark button.  Notice that point E now lies on AC. Click the close button in the new point dialog box to finish.

9.) Draw segment DE. Refer to step 4.

10.) Let us see what happens if we drag the vertices of the triangle. To drag the vertices of the triangle, click the drag vertices option button on the toolbar, then drag the vertices of the triangle.

11.) Now, we will display the length of DE and BC. To display the length of DE. To do this, click the Meas menu to display the measurements dialog box. Type DE in text box of the measurements dialog box and then click the ENTER key.

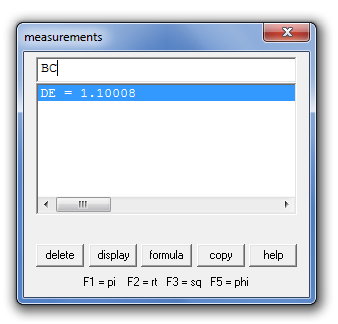
Figure 5 – The measurements dialog box.

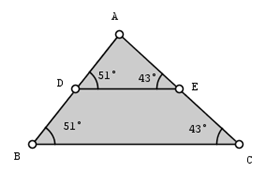
12.)  Next type BC in the text box and then press the ENTER key. What can you observe about the lengths of segments BC and DE?

13.) Select the drag vertices option button on the toolbar and drag the vertices of the triangle.  Is your observation still the same?

14.) Next, we will try to observe the relationship among the interior angles of two triangles – triangle ABC and triangle ADE. First we will display the measure of angle ABC. To do this, type <ABC in the text box of the measurements dialog box and press the ENTER key.

15.) Display the measures of the following angles using step 14: ADE, AED and ACB.

16.) What do you observe about the measures of the interior angles of triangle ABC?

17.) Close the measurements dialog box and drag the vertices of the triangle (refer to step 13). Are your observations still the same?

18.) Based on your observations, make a conjecture about the relationship of triangle ABC and its midline DE.

19.) Prove your conjectures.

4 comments , , , , , , ,

CaR Tutorial 2 – The MidSegment Theorem

Compass and Ruler, High School Geometry, Software Tutorials

In the previous CaR tutorial, we constructed and isosceles triangle. In this tutorial we are going to explore the properties of the segment connecting the midpoints of its two sides. In this tutorial we are going to learn the following:

  • use the move tool, triangle tool and segment tool
  • find the midpoint of two a segment
  • measure angles using the angle tool
  • edit properties and reveal measures of angles and segments

Construction Steps

1.) Open CaR. We will not need the Coordinate axes so click the Show grid icon until the Show the Grid icon until the grid or axes is not shown.
2.) Click the Triangle tool and click three different points on the drawing pad.
3.) Click the Move tool and right click one of the points to display the Edit Point dialog box. In the Name text box, change the name to A, then click the Show object names button (enclosed with red ellipse in Figure 1).

Figure 1 – The Edit Point dialog box.
4.) Change the name of the other two points to B and C.
5.) Click the midpoint tool, click point A and click point B to get the midpoint of AB. Now, get the midpoint of BC. Rename the midpoint of AB to E and the midpoint of AC to F (Refer to step 3). Your drawing should look like Figure 2.

Figure 2 – Triangle ABC with midpoints D and E.
6.) Right click and drag the labels to adjust their positions. Using the Move tool, move the vertices of the triangle. What do you observe?
7.) We will see the relationship of the angles and the segments in triangle ABC. We will measure the angle first. To measure angle ADE, click the points in the following order: point A, point B and point C. After this step, you will see the angle symbol at angle ADE.
8.) To display the measure of the angle, click the Move tool and right click the angle symbol. This will display the Edit Angle dialog box shown in Figure 2.
9.) To display the measure of the angle, click the Show object values icon. Then click the smallest angle symbol size to reduce the angle size. Now, click the OK button to apply changes.

Figure 3 – The Edit Angle dialog box.
10.)  Using step 8-9, measure angles ABC, ACB and AED. After measuring, your drawing should look like the figure below.
11.)  Using the Move tool, drag the vertices of the triangle. What do you observe?
12.)  Based on the measures of the angles shown in your drawing, what can you say about segment DE and segment BC?
13. ) Now, we will see if there is a relationship between the length of the segments in triangle ABC. To reveal the measure of DE, use the Move tool and right click the segment. This will reveal the Edit Line, Ray, Segment dialog box as shown in Figure 3.

Figure 5 - The Edit Line, Ray, Segment dialog box.
14.)  In the Edit Line, Ray, Segment dialog box, click the Show object values button.
15.)  Using steps 13-14, display the length of segment BC.
16.)  What can you observe about the relationship of segments DE and BC?
17.)  Move the vertices of the triangle. Are your observations still the same?
18.)  Make a conjecture about your observations above.
One comment , , , , , ,