Area Tutorial 3 – Area of a Parallelogram
In the previous area computation tutorials, we have learned how to compute the area of a rectangle and the area of a triangle. In this tutorial, we are going to learn how to compute the area of a parallelogram.
In Figure 1, we have parallelogram ABCD with given base and the dashed segment as its height. If we drop down a vertical segment from point C and extend a horizontal segment from D to the right, we can form triangle CDF as shown in Figure 2.
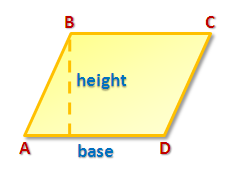
Figure 1 – Parallelogram ABCD with a given base and height.
Now, angle ABE is congruent to angle DCF (Why?), AB is congruent to CD, and angle BAE is congruent to angle CDF. Hence, by ASA congruence postulate, triangle ABE is congruent to triangle DCF.
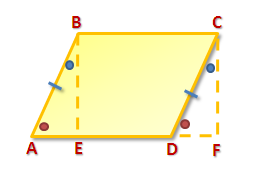
Figure 2 - ...
Since triangle BAE is congruent to triangle CDF, we can move ABE to coincide with DCF forming the rectangle in Figure 3. Click here to explore the translation using GeoGebra.
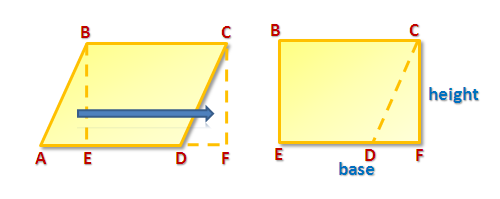
Figure 3 – Triangle ABE is translated and is superimposed to triangle CDF.
Since BCFE is a rectangle, its area therefore is the product of its base (length) and its height (width). We removed nothing from the parallelogram, therefore, the area of the parallelogram is the same as that of the area of the rectangle. Thus, the area of a parallelogram is the product of its base and its height.
Mr. Pilarski has almost a similar explanation but in video format.
Enjoy and Learn More