An Intuitive Introduction to Limits
Limits is one of the most fundamental concepts of calculus. The foundation of calculus was not entirely solid during the time of Leibniz and Newton, but later developments on the concept, particularly the definition by Cauchy, Weierstrass and other mathematicians established its firm foundation. In the discussion below, I shall introduce the concept of limits intuitively as it appears in common problems. For a more rigorous discussion, you can read the post article titled “An extensive explanation about the
definition of limits”.
Circumference and Limits
If we are going to approximate the circumference of a circle using the perimeter of an inscribed polygon, even without computation, we can observe that as the number of sides of the polygon increases, the better the approximation. In fact, we can make the perimeter of the polygon as close as we please to the circumference of the circle by choosing a sufficiently large number of sides. Notice that no matter how large the number of sides our polygon has, its perimeter will never exceed or equal the circumference of the circle.
Figure 1 – As the number of side of the polygons increases, its perimeter gets closer to the circumference of the circle.
In a more technical term, we say that the limit of the perimeter of the inscribed polygon as the number of its sides increases without bound (or as the number of sides of the inscribed polygon approaches infinity) is equal to the circumference of the circle. In symbol, if we let be the number of sides of the inscribed polygon,
be the perimeter of a polygon with
sides, and
be the circumference of the circle, we can say that the limit of
as
is equal to
. Compactly, we can write
.
Functions and Limits
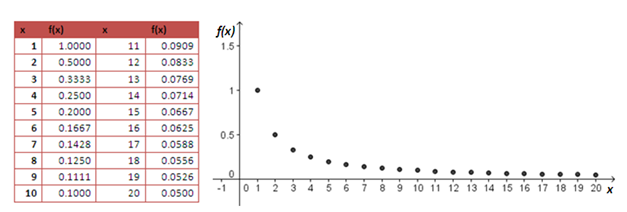
Consider the function where
is a natural number. Calculating the values of the function using the first 20 natural numbers and plotting the points in the
-plane, we arrive at the table and the graph in Figure 2.
First, we see that as the value of increases, the value of
decreases and approaches
. Furthermore, we can make the value of
as close to
as we please by choosing a sufficiently large
. We also notice that no matter how large the value of
is, the value of
will never reach
.
Hence, we say that the limit of as the value of
increases without bound is equal to
, or equivalently the limit of
as
approaches infinity is equal to
. In symbol, we write the limit of
as
or more compactly the
.
Tangent line and Limits
Recall that the slope of a line is its “rise” over its “run”. The formula of slope of a line is
, given two points with coordinates
and
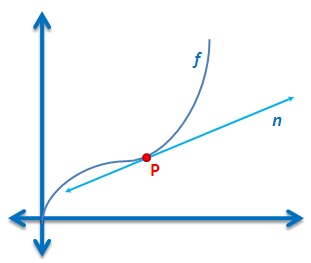
. One of the famous ancient problems in mathematics was the tangent problem, which is getting the slope of a line tangent to a function at a point. In the Figure 3, line
is tangent to the function
at point
.
If we are going to compute for the slope of the line tangent line, we have a big problem because we only have one point, and the slope formula requires two points. To deal with this problem, we select a point on the graph of
, draw the secant line
and move
along the graph of
towards
. Notice that as
approaches
(shown as
and
), the secant line gets closer and closer to the tangent line. This is the same as saying that the slope the secant line is getting closer and closer to the slope of the tangent line. Similarly, we can say that as the distance between the x-coordinates of
and
is getting closer and closer to
, the slope of the secant line is getting closer and closer to the slope of the tangent line.
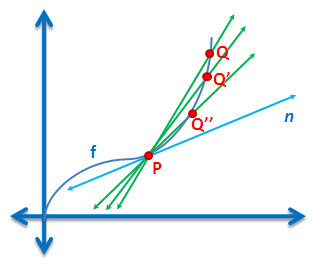
Figure 4 – As point Q approaches P, the slope of the secant line is getting closer and closer to the slope of the tangent line.
If we let be the distance between the x-coordinates of
and
,
be the slope of the secant line
and
be the slope of the tangent line, we can say that the limit of the slope of secant line as
approaches
is equal to the slope of the tangent line. Concisely, we can write
.
Area and Limits
Another ancient problem is about finding the area under a curve as shown in the leftmost graph in Figure 5. During the ancient time, finding the area of a curved plane was impossible.
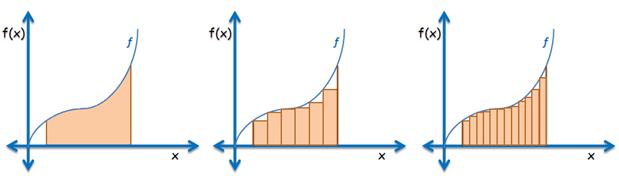
Figure 5 – As the number of rectangles increases, the sum of the area of the rectangles is getting closer and closer to the area of the bounded plane under the curve.
We can approximate the area above in the first graph in Figure 5 by constructing rectangles under the curve such that one of the corners of the rectangle touches the graph as shown in the second and third graph in Figure 5. We can see that as we increase the number of rectangles, the better is our approximation of the area under the curve. We can also see that no matter how large the number of rectangles is, the sum its areas will never exceed (or equal) the area of the plane under the curve. Hence, we say that as the number of rectangles increases without bound, the sum of the areas of the rectangles is equal to the area under the curve; or the limit of the sum of the areas of the rectangles as the number of rectangles approaches infinity is equal to the area of the plane under the curve.
If we let be the area under the curve,
be the sum of the areas of
rectangles, then we can say that the limit of
as n approaches infinity is equal to
. Concisely, we can write
.
Numbers and Limits
We end with a more familiar example usually found in books. What if we want to find the limit of as
approaches
?
To answer the question, we must find the value where
is very close to
. Those values would be numbers that are very close to
– some slightly greater than
and some slightly less than
. Place the values in a table we have
From the table, we can clearly see that as the value of approaches
, the value of
approaches
. Concisely, we can write the
.
Mr. Jayson Dyer, author of The Number Warrior has another excellent explanation on the concept of limits in his blog Five intuitive approaches to teaching the infinitely small.
******
The area under the curve problem and the tangent problem are the ancient problems which gave birth to calculus. Calculus was independently invented by Gottfried Leibniz and Isaac Newton in the 17th century.