Tag: GeoGebra Ray Through Two Points

GeoGebra Essentials 5 – The Compass Tool and the SSS Congruence

GeoGebra, High School Geometry, High School Mathematics

This is the fifth tutorial in the GeoGebra Essentials Series. If you are not familiar with GeoGebra, you may want to read the Introduction to GeoGebra post and prior tutorials. They contain the pre-requisites of this tutorial.

In the tutorial below, menu commands, located in the menu bar, are in brown bold text, and submenus are denoted by the > symbol. For example, Options>Labeling> New Points Only means, click the Options menu, choose Labeling from the list, then select New Points Only. The tool texts are colored orange. For example, New Point means the new point tool.

geogebra - triangle congruence

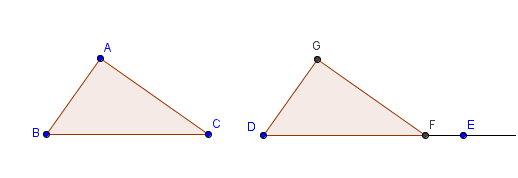
In this tutorial, we will mimic compass and straightedge construction using GeoGebra’s Compass tool, Segment and Ray tools. We use the concept of the SSS congruence1 to construct a triangle congruent to a given triangle. » Read more

4 comments , , , , ,

GeoGebra Tutorial 27 – Animation and Epicycle

GeoGebra, Software Tutorials

This is the 27th tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, you might want to read the GeoGebra Essentials Series.

In this tutorial, we rotate a circle about the center of another circle tangent to it using the animation feature of GeoGebra. Along the rotating circle, we will also rotate a point on its circumference about its center (see red point in the diagram). The path of this point is called the epicycloid.

If you want to follow this tutorial step-by-step, you can open the GeoGebra window in your browser by clicking here.  You can view the output of this tutorial here. » Read more

Leave a comment , , , , , ,

GeoGebra Tutorial 30 – Loci, Roses and Reflections

GeoGebra, Software Tutorials

This is the 30th GeoGebra Tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, you might want to read the GeoGebra Essentials Series.

In this tutorial, we reflect a point on a unit circle about the x-axis and about the y-axis to form rectangle ABCD. We construct a segment with length equal to the area of the rectangle passing through point B.  One of the endpoints of this segment is at the origin.  As we move the point B along the the circle, the trace of the end point of the segment that not on the circle’s center will form a 4-petal rose.

If you want to follow this tutorial step-by-step, you can open the GeoGebra window in your browser by clicking here.  You can view the output of this tutorial here. » Read more

Leave a comment , , , , , , , ,
1 2