Tag: parallelogram area

Area Tutorial 4 – Derivation of the Area of a Circle

Elementary School Geometry, Elementary School Mathematics

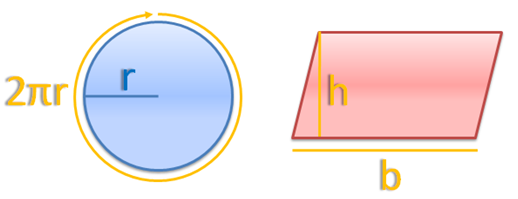
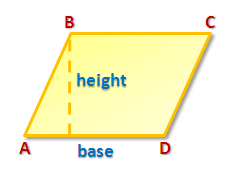
We have learned that the area of a parallelogram is the product of its base and its height, and the circumference of a circle with radius r is 2 \pi r.

Figure 1 – A circle with radius r and a parallelogram with base b and altitude h.

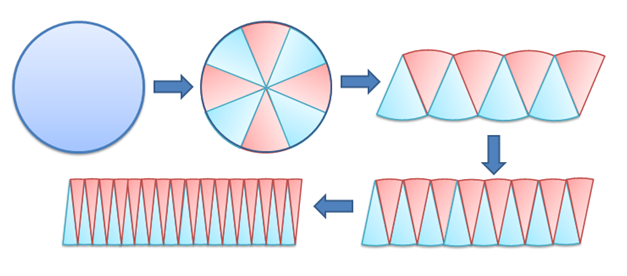
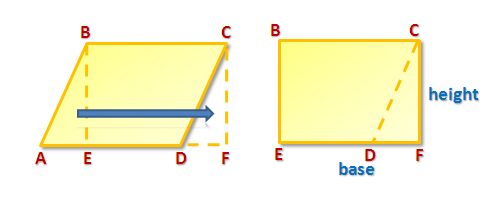
To find the area of a circle with radius r, divide it into congruent sectors (blue and red divisions) then arrange them as shown below.

Figure 2 – As the number of sectors increases, the shape of the rearranged sector is becoming more and more parallelogram-like.

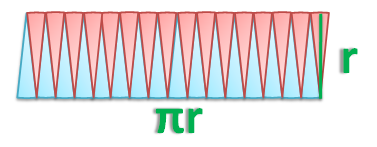
Observe that as the number of sectors increases, the shape of the rearranged sectors is becoming more and more like a parallelogram. In fact, if we can divide the circle into an infinite a number of sectors, it seems that the shape of the rearranged sector is a parallelogram.  Assuming that this is true, then the base of a parallelogram is \pi r  (Explain why.), and its altitude is r.

Figure 3 – The base of the parallelogram is pi*r and its height is r.

Since the area of a parallelogram is bh, we just have to multiply the base of the parallelogram which is \pi r and its height which is r to find its area. Therefore, the area of the parallelogram, which is equal to the area of a circle, is \pi r^2.

Another derivation

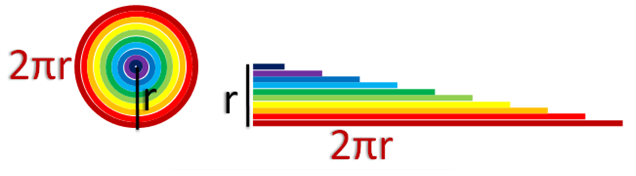
We can also derive the area of a circle by unwinding an infinite number of circular tracks. The smaller the width of our track becomes, the rearranged figure becomes more and more like a triangle. If it is indeed a triangle, then its area is the product of its height and its width.

Figure 4 – The base of the parallelogram is pi*r and its height is r.

Recall that the area of a triangle is the product of its base and height divided by 2.  Since the base of the of the triangle is equal to the circumference of the circle  (2 \pi r), and its height is equal to its radius (r), therefore, the area of the triangle, which is equal to the area of the circle, is \displaystyle\frac{(2 \pi r)(r)}{2} = \pi r^2.

The processes that we have done above are logical; however,  we only assumed that we can divide the circle into infinite number of sectors, or we can unwind an infinite number of tracks.  These are just assumptions, hence, we are not yet sure if the area of the circle is indeed \pi r^2. Of course, we know it is true but we need a proof.  The proof finding the area of a circle needs knowledge on integral calculus. We will discuss the proof of the area of the circle in the future.

Enjoy and Learn More

6 comments , , , , , , , ,

Area Tutorial 3 – Area of a Parallelogram

Elementary School Geometry, Elementary School Mathematics

In the previous area computation tutorials, we have learned how to compute the area of a rectangle and the area of a triangle.  In this tutorial, we are going to learn how to compute the area of a parallelogram.

In Figure 1, we have parallelogram ABCD with given base and the dashed segment as its height. If we drop down a vertical segment from point C and extend a horizontal segment from D to the right, we can form triangle CDF as shown in Figure 2.

Figure 1 – Parallelogram ABCD with a given base and height.

Now, angle ABE is congruent to angle DCF (Why?), AB is congruent to CD, and angle BAE is congruent to angle CDF. Hence, by ASA congruence postulate, triangle ABE is congruent to triangle DCF.

Figure 2 - ...

Since triangle BAE is congruent to triangle CDF, we can move ABE to coincide with DCF forming the rectangle in Figure 3. Click here to explore the translation using GeoGebra.

Figure 3 – Triangle ABE is translated and is superimposed to triangle CDF.

Since BCFE is a rectangle, its area therefore is the product of its base (length) and its height (width). We removed nothing from the parallelogram, therefore, the area of the parallelogram is the same as that of the area of the rectangle. Thus, the area of a parallelogram is the product of its base and its height.

Mr. Pilarski has almost a similar explanation but in video format.

Enjoy and Learn More

6 comments , , , , , ,