Month in Review – July 2012
It’s the end of the month again. In case you missed some posts, here is the complete list of posts for July 2012. Enjoy reading!
Month in Review
- Introduction to Number Bases
- Why Expressions with Negative Exponents Equal their Reciprocals
- Wholemovement and The Art of Folding Circles
- Who’s the Winner?
- Mu Alpha Theta: 10,000+ Math Contest Problems with Solutions
- Why is negative times negative equals positive?
- Math and Multimedia Blog Carnival 22 is live
- The Magic Circle Puzzle
- The Musical Beauty of Tau
- It is an Honor to be a GeoGebra Ambassador
- Apple and the Golden Ratio?
- 11 Mathematical Proof Techniques Liberal Arts Majors Should Know
- Scribblar: A Free Online Multi-user Whiteboard
- Math Blog Carnival Reminder
- GeoGebraTube: More than 12000 applets and counting
- Math Teachers at Play 52
- Proof without Words: Odds and Squares
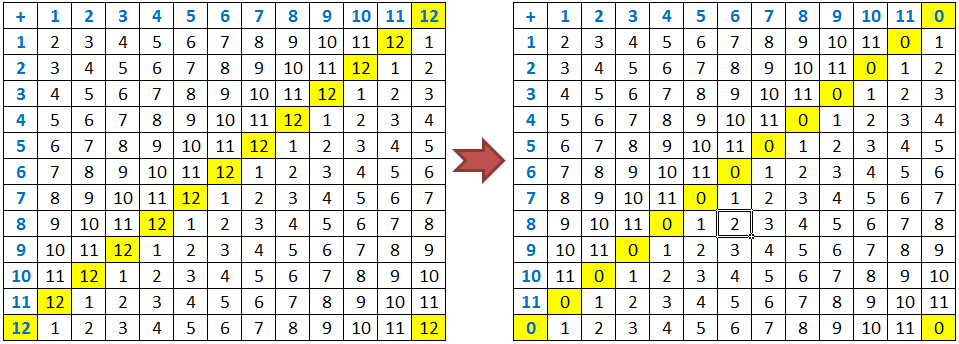
- Clock Arithmetic and Modular Systems Part 2
- Introduction to Clock Arithmetic and Modular Systems
- Sketchometry: A Geometry App To Watch Out For
- The Math and Multimedia Carnival is back
- Design your Own Mandelbrot Set
- Can you solve the hardest Sudoku puzzle yet?
Subscribe and Share
- Like Math and Multimedia on Facebook
- Follow Math and Multimedia on Twitter
- Subcribe to Math and Multimedia RSS Feeds
You might also visit my other blogs:
- Math Palette – a blog about math appreciation
- GeoGebra Applet Central – a collection of GeoGebra applets.
- Sipnayan – My math tutorial blog written in Filipino.
- School of Freebies – A blog about free software and anything free on the net.