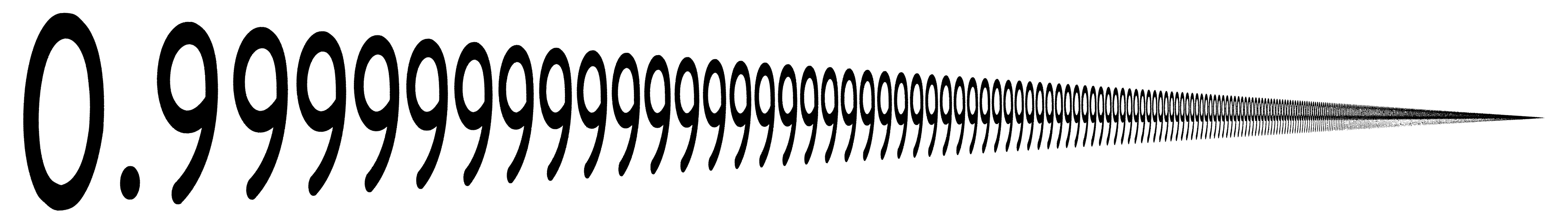College Mathematics Archives - Page 25 of 30

Geometric Sequences and Series

June 9, 2010 GB Calculus and Analysis, College Mathematics, High School Algebra, High School Mathematics

Introduction

We have discussed about arithmetic sequences, its characteristics and its connection to linear functions. In this post, we will discuss another type of sequence.

The sequence of numbers 2, 6, 18, 54, 162, … is an example of an geometric sequence. The first term 2 is multiplied by 3 to get the second term, the second term is multiplied by 3 to get the third term, the third term is multiplied by 3 to get the fourth term, and so on. The same number that we multiplied to each term is called the common ratio. Expressing the sequence above in terms of the first term and the common ratio, we have 2, 2(3), 2(3²), 2(3³), …. Hence, a geometric sequence, also known as a geometric progression, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio.

The Sierpinski triangle below is an example of a geometric representation of a geometric sequence. The number of blue triangles, the number of white triangles, their areas, and their side lengths form different geometric sequences. It is left to the reader, as an exercise, to find the rules of these geometric sequences.

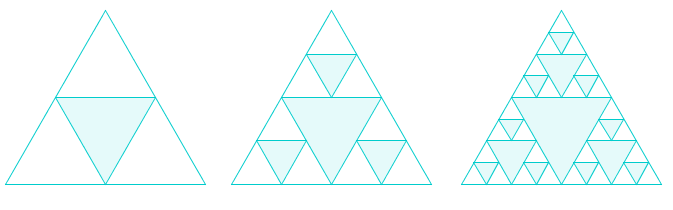
Figure 1 - The Seriepinski Triangles.

To generalize, if a₁ is its first term and the common ratio is r, then the general form of a geometric sequence is a₁, a₁r, a₁r², a₁r³,…, and the n^th term of the sequence is a₁r^n-1.

A geometric series, on the other hand, is the sum of the terms of a geometric sequence. Given a geometric sequence with terms a₁r, a₁r², a₁r³,…, the sum S_nof the geometric sequence with n terms is the geometric series a₁ + a₁r + a₁r², a₁r³ + … + ar^n-1. Multiplying S_n by -r and adding it to S_n, we have

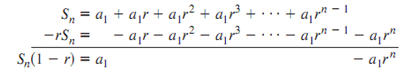
Hence, the sum of a geometric series with n terms, and $r \neq 1 = \displaystyle\frac{a_1(1-r^n)}{1-r}$ .

Sum of Infinite Geometric Series and a Little Bit of Calculus

Note: This portion is for those who have already taken elementary calculus.

The infinite geometric series $\{a_n\}$ is the the symbol $\sum_{n=1}^\infty a_n = a_1 + a_2 + a_3 + \cdots$ . From above, the sum of a finite geometric series with $n$ terms is $\displaystyle \sum_{k=1}^n \frac{a_1(1-r^n)}{1-r}$ . Hence, to get the sum of the infinite geometric series, we need to get the sum of $\displaystyle \sum_{n=1}^\infty \frac{a_1(1-r^n)}{1-r}$ . However, $\displaystyle \sum_{k=1}^\infty \frac{a_1(1-r^n)}{1-r} = \lim_{n\to \infty} \frac{a_1(1-r^n)}{1-r}$ .

Also, that if $|r| < 1$ , $r^n$ approaches $0$ (try $(\frac{2}{3})^n$ or any other proper fraction and increase the value of $n$ ), thus, $\displaystyle \sum_{n=1}^\infty \frac{a_1(1-r^n)}{1-r} = \lim_{n \to \infty} \frac{a_1(1-r^n)}{1-r} = \frac{a_1}{1-r}$ . Therefore, sum of the infinite series $\displaystyle a_1 + a_2r + a_2r^2 + \cdots = \frac{a_1}{1-r}$ .

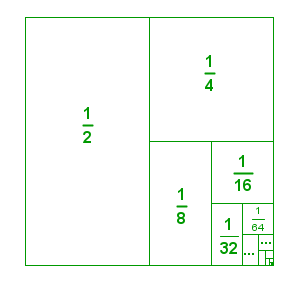
One very common infinite series is $\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$ , or the sum of the areas of the partitions of the square with side length 1 unit shown below. Using the formula above,

$\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n} = \frac{a_1}{1-r} = \frac{\frac{1}{2}}{1-\frac{1}{2}} = 1$ .

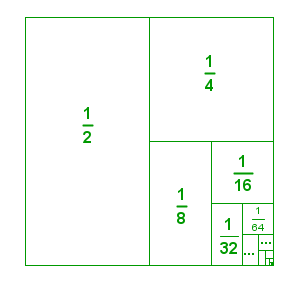
Figure 2 - A representation of an infinite geometric series.

This is evident in the diagram because the sum of all the partitions is equal to the area of a square. We say that the series $\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n}$ converges to 1.

8 comments common ratio, geometric progressions, geometric sequence, infinite geometric sequence, sierpinski triangle, sum of infinite geometric series

Is 0.999… really equal to 1?

June 4, 2010 GB Calculus and Analysis, High School Calculus

Introduction

Yes it is. 0.999… is equal to 1.

Before we begin our discussion, let me make a remark that the symbol “…” in the decimal 0.999… means that the there are infinitely many 9’s, or putting it in plain language, the decimal number has no end.

A Friendly Chat About Whether 0.999… = 1 | BetterExplained via kwout

For non-math persons, you will probably disagree with the equality, but there are many elementary proofs that could show it, some of which, I have shown below. A proof is a series of valid, logical and relevant arguments (see Introduction to Mathematical Proofs for details), that shows the truth or falsity of a statement.

Proof 1

$\frac{1}{3} = 0.333 \cdots$

$\frac{2}{3} = 0.666 \cdots$

$\frac{1}{3} + \frac{2}{3} = 0.333 \cdots + 0.666 \cdots$

$\frac{3}{3} =0.999 \cdots$

But $\frac{3}{3} = 1$ , therefore $1 =0.999 \cdots$

Proof 2

$\frac{1}{9} = 0.111 \cdots$
Multiplying both sides by 9 we have

$1 = 0.999 \cdots$

Proof 3

Let $x = 0.999 \cdots$

$10x = 9.999 \cdots$

$10x - x = 9.999 \cdots - 0.9999 \cdots$

$9x = 9$

$x = 1$

Hence, $0.999 \cdots = 1$

Still in doubt?

Many will probably be reluctant in accepting the equality $1 = 0.999 \cdots$ because the representation is a bit counterintuitive. The said equality requires the notion of the real number system, a good grasp of the concept of limits, and knowledge on infinitesimals or calculus in general. If, for instance,you have already taken sequences (in calculus), you may think of the $0.999 \cdots$ as a sequence of real numbers $(0.9, 0.99, 0.999,\cdots)$ . Note that the sequence gets closer and closer to 1, and therefore, its limit is 1.

Infinite Geometric Sequence

My final attempt to convince you that $0.999 \cdots$ is indeed equal to $1$ is by the infinite geometric sequence. For the sake of brevity, in the remaining part of this article, we will simply use the term “infinite sequence” to refer to an infinite geometric sequence. We will use the concept of the sum of an infinite sequence, which is known as an infinite series, to show that $0.999 \cdots = 1$ .

One example of an infinite series is $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$ . If you add its infinite number of terms, the answer is equal to 1. Again, this is counterintuitive.

How can addition of numbers with infinite number of terms have an exact (or a finite) answer?

There is a formula to get the sum of an infinite geometric sequence, but before we discuss the formula, let me give the geometric interpretation of the sum above. The sum $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$ can be represented geometrically using a 1 unit by 1 unit square as shown below. If we divide the square into two, then we will have two rectangles, each of which has area $\frac{1}{2}$ square units. Dividing the other half into two, then we have three rectangles with areas $\frac{1}{2}$ , $\frac{1}{4}$ , $\frac{1}{4}$ square units. Dividing the one of the smaller rectangle into two, then we have four rectangles with areas $\frac{1}{2}$ , $\frac{1}{4}$ , $\frac{1}{8}$ , $\frac{1}{8}$ . Again, dividing one of the smallest rectangle into two, we have five rectangles with areas $\frac{1}{2}$ , $\frac{1}{4}$ , $\frac{1}{8}$ , $\frac{1}{16}$ , and $\frac{1}{16}$ Since this process can go on forever, the sum of all the areas of all the rectangles will equal to 1, which is the area of the original square.

Now that we have seen that an infinite series can have a finite sum, we will now show that $0.999 \cdots$ can be expressed as a finite sum by expressing it as an infinite series. The number $0.999 \cdots$ can be expressed as an infinite series $0.9 + 0.09 + 0.009 + \cdots$ . Converting it in fractional form, we have $\frac{9}{10} + \frac{9}{100} + \frac{9}{1000} + \cdots$ .

We have learned that the sum of the infinite series with first term $\displaystyle a_1$ and ratio $r$ is described by $\displaystyle\frac{a_1}{1-r}$ . Applying the formula to our series above, we have

$\displaystyle\frac{\frac{9}{10}}{1-\frac{1}{10}} = 1$

Therefore, the sum our infinite series is 1.

Implication

This implication of the equality $0.999 \cdots =1$ means that any rational number that is a non-repeating decimal can be expressed as a repeating decimal. Since $0.999 \cdots =1$ , it follows that $0.0999 \cdots =0.1, 0.00999 \cdots=0.01$ and so on. Hence, any decimal number maybe expressed as number + 0.00…01. For example, the decimal $4.7$ , can be expressed as $4.6 + 0.1 = 4.6 + 0.0999 \cdots = 4.6999 \cdots$ . The number $0.874$ can also be expressed as $0.873 + 0.001 = 0.873 + 0.000999 \cdots = 0.873999 \cdots$

Conclusion

Any of the four proofs above is actually sufficient to show that $0.999 \cdots = 1$ . Although this concept is quite hard to accept, we should remember that in mathematics, as long as the steps of operations or reasoning performed are valid and logical, the conclusion will be unquestionably valid.

There are many counterintuitive concepts in mathematics and the equality $0.999 \cdots = 1$ is only one of the many. In my post, Counting the Uncountable: A Glimpse at the Infinite, we have also encountered one: that the number of integers (negative, 0, positive) is equal to the number of counting numbers (positive integers) and we have shown it by one-to-one pairing. We have also shown that the number of counting numbers is the same as the number of rational numbers. Thus, we have shown that a subset can have the same element as the “supposed” bigger set. I guess that is what makes mathematics unique; intuitively, some concepts do not make sense, but by valid and logical reasoning, they perfectly do.

Notes:

You can find discussions about 0.999… = 1 here and here.
There is another good post about it here and here.

Related Articles

9 comments 0.999 equals 1, 0.999... does not equal 1, 0.999... exactly equals 1, 0.999...=1, concept of limits, counting numbers, does 0.999 1, infinite geometric sequence, infinite geometric series, limits and infinitesimals, mathematical proofs, rational numbers, real number system, repeating decimal, sequence of real numbers

Counting the Uncountable: A Glimpse at Infinite Sets

May 10, 2010 GB College Mathematics, Set Theory

When counting, we pair the counting numbers (positive integers) with the objects that we are counting. For example, when we count our fingers, we assign a corresponding number to each finger. A possible assignment would be 1 to the pinkie, 2 to the ring finger, 3 to the middle finger, 4 to the index finger, and 5 to the thumb. Of course, the order does not matter as long as we have a one-to-one pairing. As we can see, counting is easy once the objects that we are counting is finite.

Higher mathematics, however, does not just deal with finite number of objects. Sometimes, mathematicians need to examine sets of objects with infinite number of elements. Such sets are called infinite sets. The set of integers Z and the set of counting numbers N are examples of infinite sets.

One strategy used to examine the number of elements in an infinite set is to find another infinite set that is easier to enumerate, then compare them. If a strategy can be done such that each element in the first set can be paired with exactly one element in the second set without missing anything, then it follows that the two sets have the same number of elements.

alg_shoes.jpg (JPEG Image, 450×321 pixels) via kwout

This may sound a little absurd at first, but let us have the following analogy: If we want to know how many pairs of shoes are available in a shoe store, we do not have to count all the shoes. We can just count the number of left-foot shoes, and we will know how many shoes are there. Our assumption, of course, is that every shoe has a pair.

Table 1 – Counting Numbers and Integers Pairing

With the abovementioned strategy, let us try to compare the set of counting numbers N and the set of the integers Z. In Table 1, it is clear each element in N can be paired with exactly one element in Z, such that N is in increasing order and Z in alternating positive an negative signs. As we can see, this strategy will not miss any integer as N increases without bound. It is also apparent that even if the pairing continues forever, we are sure that each element in N has a pair in Z. Hence, the number positive integers N is the same as the number of all the integers Z including 0 and negative!

Surprised?

This is also the same with rational numbers. The number of elements in the set of positive rational numbers Q is the same as the number elements in the set of counting numbers N. In Table 2, we can see the first 15 pairs of the one-to-one pairing. There are duplicates such as 1/2 and 2/4, but we can easily eliminate equivalent fractions and replace them with the next rational numbers. From the table, it is easy to see that we can devise a way to pair the set N (red texts) with the set Q (yellow texts) without missing anything.

Can you see the pattern?

Therefore, we can conclude that the number of positive rational numbers are as many as the number of counting numbers.

Table 2 – Counting numbers and rational numbers pairing.

From our discussion above, we can conclude that the set of counting numbers N, the set of integers Z, and the set of rational numbers Q have the same number of elements.

Going Technical

In set theory, the number of elements of a set is called cardinality. Hence the cardinality of the set of vowel letters in the English alphabet {A, E, I, O, U} is 5, and the cardinality of the set of binary numbers {1,0} is 2.

Venn Diagram of the set of N, Z and Q.

It is interesting to note that there is a little bit of irony in our discussion above. We know that N is a subset of Z, and Z is a subset of Q, yet the three sets have the same cardinality.

The symbol $\aleph_0$ (or aleph null) is the symbol assigned to the cardinality of counting numbers.

Leave a comment bijections, cardinality of sets, comparing two infinite sets, infinite sets

« 1 … 23 24 25 26 27 … 30 »