High School Number Theory Archives - Page 6 of 11

A Simple Proof of the Arithmetic Mean Geometric Mean Inequality

May 16, 2012 GB High School Mathematics, High School Number Theory

Last February, we have used area to prove the Arithmetic Mean – Geometric Mean Inequality (AM-GM Inequality). In this post, we show a simpler proof.

Click image view the GeoGebra applet demonstration

Recall that the AM-GM Inequality states that given two numbers, their geometric mean is always less than or equal to their arithmetic mean. That is given two numbers $a$ and $b$ ,

$\displaystyle\sqrt{ab} \leq \frac{a+b}{2}$ . » Read more

3 comments am gm inequality proof, arithmetic geometric mean inequality, mathematical proof

Another Proof of the Sum of the First n Positive Integers

April 30, 2012 GB High School Mathematics, High School Number Theory

We have discussed how Gauss was able to devise a clever way to add the first $100$ positive integers at a very young age in a few minutes. We generalized his method and have also seen the link between the sum and the area of a triangle. In both discussions, we have shown that the sum of the first $n$ positive integers is $\frac{n(n+1)}{2}$ .

In this post, we discuss another geometric proof of the problem above. We start with a specific case adding the first $6$ positive integers, and the proceed to the general case.

We can add the first $6$ positive integers manually or just by counting the number of unit squares in the figure above. The figure shows the geometric representation of the sum of the first 6 positive integers. Adding manually is not difficult if the given is small. However, we need a strategy for larger numbers. » Read more

4 comments mathematical proof, sum of first n counting numbers, sum of first n natural numbers, sum of first n positive integers

Divisibility by 9

April 19, 2012 GB High School Mathematics, High School Number Theory

This is the 8th part of the Divisibility Rules Series. In this post, we discuss divisibility by 9.

When 10 is divided by 9, it gives a remainder of 1 since 10 = 9 + 1. Also, 100 divided by 9 gives a remainder of 1 since 100 = 99 + 1. Further, 1000 gives a remainder of 1 when divided by 9 since it can be expressed as 999 + 1. From the pattern, we can see that powers of 10 give a remainder of 1 when divided by 9 since they can be expressed as 999…9 + 1.

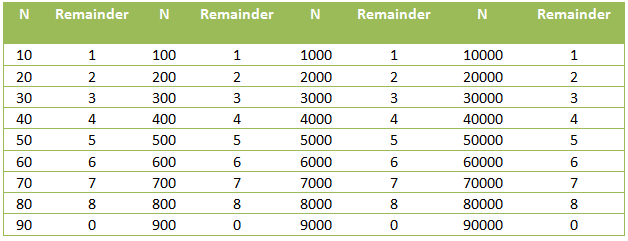
In addition, observe from the table that 20 divided by 9 is equal to 2, and 300 divided by 9 = 3, 5000 divided by 9 = 5. We can see that a positive integer n less than 9 multiplied by a power of 10 gives a remainder of n when divided by 9. Now since 3465 can be expressed as 3000 + 4000 + 60 + 5 = 3(10³) + 4(10²) + 6(10¹) + 5(10⁰), we can use the expanded form to determine divisibility by 9. For example, in the second table, the remainders of the expansion are 3, 4, 6, and 5. We now take the sum of these remainders and see if they are divisible by 9. » Read more

One comment divisibility by 9, divisibility rules, divisibility rules series, divisibility tests

« 1 … 4 5 6 7 8 … 11 »