High School Mathematics Archives - Page 149 of 157

The Algebraic and Geometric Proofs of Pythagorean Theorem

February 3, 2010 GB High School Geometry, High School Mathematics

The Pythagorean Theorem states that if a right triangle has side lengths $a, b$ and $c$ , where $c$ is the hypotenuse, then the sum of the squares of the two shorter lengths is equal to the square of the length of the hypotenuse.

Figure 1 – A right triangle with side lengths a, b and c.

Putting it in equation form, we have

$a^2 + b^2 = c^2$ .

For example, if a right triangle has side lengths $5$ and $12$ , then the length of its hypotenuse is $13$ , since $c^2 = 5^2 + 12^2 \Rightarrow c = 13$ .

Exercise 1: What is the hypotenuse of the triangle with sides $1$ and $\sqrt{3}$ ?

The converse of the theorem is also true. If the side lengths of the triangle satisfy the equation $a^2 + b^2 = c^2$ , then the triangle is right. For instance, a triangle with side lengths $(3, 4, 5)$ satisfies the equation $3^2 + 4^2 = 5^2$ , therefore, it is a right triangle.

Geometrically, the Pythagorean theorem states that in a right triangle with sides $a, b$ and $c$ where $c$ is the hypotenuse, if three squares are constructed whose one of the sides are the sides of the triangle as shown in Figure 2, then the area of the two smaller squares when added equals the area of the largest square.

Figure 2 – The geometric interpretation of the Pythagorean theorem states that the area of the green square plus the area of the red square is equal to the area of the blue square.

One specific case is shown in Figure 3: the areas of the two smaller squares are $9$ and $16$ square units, and the area of the largest square is $25$ square units.

Exercise 2: Verify that the area of the largest square in Figure 3 is 25 square units by using the unit squares.

Figure 3 – A right triangle with side lengths 3, 4 and 5.

Similarly, triangles with side lengths $(7, 24, 25)$ and $(8, 15, 17)$ are right triangles. If the side lengths of a right triangle are all integers, we call them Pythagorean triples. Hence, $(7, 24, 25)$ and $(8, 15, 17)$ are Pythagorean triples.

Exercise 3: Give other examples of Pythagorean triples.

Exercise 4: Prove that there are infinitely many Pythagorean triples.

Proofs of the Pythagorean Theorem

There are more than 300 proofs of the Pythagorean theorem. More than 70 proofs are shown in tje Cut-The-Knot website. Shown below are two of the proofs. Note that in proving the Pythagorean theorem, we want to show that for any right triangle with hypotenuse $c$ , and sides $a$ , and $b$ , the following relationship holds: $a^2 + b^2 = c^2$ .

Geometric Proof

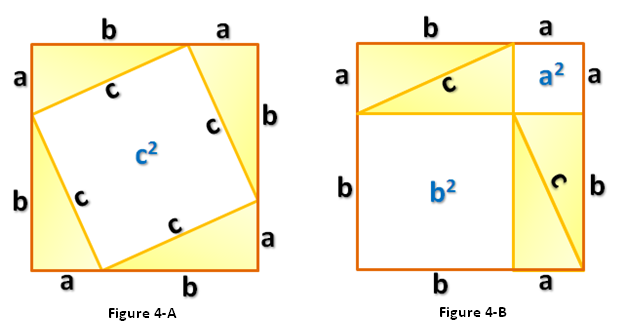
First, we draw a triangle with side lengths $a, b$ and $c$ as shown in Figure 1. Next, we create 4 triangles identical to it and using the triangles form a square with side lengths $a + b$ as shown in Figure 4-A. Notice that the area of the white square in Figure 4-A is $c^2$ .

Figure 4 – The Geometric proof of the Pythagorean theorem.

Rearranging the triangles, we can also form another square with the same side length as shown in Figure 4-B.This means that the area of the white square in the Figure 4-A is equal to the sum of the areas of the white squares in Figure 4-B (Why?). That is, $c^2 = a^2 + b^2$ which is exactly what we want to show. *And since we can always form a (big) square using four right triangles with any dimension (in higher mathematics, we say that we can choose arbitrary $a$ and $b$ as side lengths of a right triangle), this implies that the equation $a^2 + b^2 = c^2$ stated above is always true regardless of the size of the triangle.

Exercise 5: Prove that the quadrilateral with side length C in Figure 4-A is a square.

Algebraic Proof

In the second proof, we will now look at the yellow triangles instead of the squares. Consider Figure 4-A. We can compute the area of a square with side lengths $a + b$ using two methods: (1) we can square the side lengths and (2) we can add the area of the 4 congruent triangles and then add them to the area of the white square which is $c^2$ . If we let $A$ be the area of the square with side $b + a$ , then calculating we have

Method 1: $A = (b + a)^2 = b^2 + 2ab +a^2$

Method 2: $A = 4(1/2ab) + c^2 = 2ab + c^2$

Methods 1 and 2 calculated the area of the same square, therefore they must be equal. This means that we can equate both expressions. Equating we have,

$b^2 + 2ab + a^2 = 2ab + c^2 \Rightarrow a^2 + b^2 = c^2$

which is exactly what we want to show.

Leave a comment algebraic proofs, geometric proofs, proof of pythagorean theorem, pure mathematics, pythagora's theorem, pythagorean theorem, pythagorean triples, right heron triangles, right triangles

Is there an SSA Congruence?

January 29, 2010 GB High School Geometry, High School Mathematics

In the Triangle Congruence post, we discussed about ways to test if two triangles are congruent. The only theorems (or sometimes called postulates) that hold are the SSS, SAS and ASA congruence. We ended our discussion with the question about the AAS (or SAA), AAA and SSA (or ASS) congruence.

Let us try to explore the AAS case. If we have two triangles (see first pair of in Figure 1), and two pairs of their angles (denoted by the blue and red circles) are congruent the third pair of angles (denoted by the yellow circles in the second pair) are also congruent. Hence, a pair of sides (both included in two pairs of congruent angles) are congruent, which is similar to the ASA congruence. Therefore AAS congruence holds and is equivalent to ASA congruence.

Figure 1 – AAS and ASA congruence postulates are equivalent.

In Figure 2, shown are triangles with three pairs of angles that are congruent. It is clear that the two triangles are not congruent. Therefore, AAA congruence does not hold.

Figure 2 – Triangles having three pairs of congruent angles.

Now, let us try the SSA congruence. Figure 3-A shows triangle ABC with sides and angle marked. We extend AC to the right hand side (see Figure 3-B), then rotate BC about point B (see Figure 3-C). We let C’ be the intersection of BC and the extended segment such that BC is congruent to BC’ (see Figure 3-D).

Figure 3 – Triangels having two pairs of sides and a pair of angles which are congruent.

Looking at Figure 3-A and Figure 3-D, two pairs of their sides and a pair of non-included angles are congruent, but the triangles are not congruent. Therefore, SSA (or ASS) congruence does not hold.

13 comments congruence geometry, congruent triangles, congruent triangles ssa, side angle congruence, side side angle congruence, SSA congruence, SSA triangle congruence

A Closer Look at the Midpoint Formula

January 20, 2010 GB High School Algebra, High School Geometry, High School Mathematics

Introduction

If we want to find the midpoint of segment CD in Figure 1, where the coordinates of points C and D are $(-2,5)$ and $(-2,1)$ , it is clear that the length of CD is $5 - 1 = 4$ units. To determine the midpoint of CD, we want to get the coordinates of the point which is $2$ units away from both points C and D. Hence, we have to divide $5 - 1 = 4$ by $2$ , and add the result to $1$ or subtract the result from $5$ . Summarizing, the expression that would describe the value of the y-coordinate of the midpoint would be $\displaystyle\frac{(5 - 1)}{2} + 1$ or $5 - \displaystyle\frac{(5 - 1)}{2}$ . This means that the midpoint of CD is $(0,2)$ .

If we want to get the midpoint of AB, using the same reasoning above, the expression that would describe the x-coordinate of the midpoint would be $\displaystyle\frac{(6 - 3)}{2} + 3$ or $6 - \displaystyle\frac{(6 - 3)}{2}$ . This means that the midpoint of AB is $(1.5,0)$ .

Figure 1 – Horizontal line AB and vertical line CD in the coordinate plane.

Generalizing our observation above, if we have a vertical segment with their endpoints having coordinates $(a, y_1)$ and $(a,y_2)$ (see Figure 2), we can get its midpoint using the following formula $\displaystyle\frac{y_2 - y_1}{2} + y_1$ or $y_2 - \displaystyle\frac{y_2 - y_1}{2} + y_1$

Figure 2 – Generalized coordinates of a vertical and a horizontal line.

Simplifying, both the expressions above result to $\displaystyle\frac{y_2 + y_1}{2}$ . Similarly, for a horizontal segment with endpoints having coordinates $(x_1, b)$ and $(x_2, b)$ can be computed by the expression $\displaystyle\frac{x_1 + x_2}{2}$ .

Midpoint of a Slanting Segment

The preceding derivations are only valid for vertical and horizontal segments. In Figure 3, segment AB is neither horizontal nor vertical. To investigate the midpoint of AB, we draw vertical segment PQ coinciding with the y-axis with endpoints having y-coordinates the same as those of the y-coordinates of segment AB (see Figure 3). We also draw a horizontal line RS coinciding the x-axis with endpoints having x-coordinates the same as those of the x-coordinates of segment AB. Looking at Figure 3, it is clear that the coordinates of the midpoint of the PQ is $(0,3)$ .

If we draw a horizontal line from $(0,3)$ towards segment AB (see yellow dashed segment), and draw a vertical line from the intersection M to segment RS, it seems that the intersection of the yellow dashed line and segment RS is $(3.5,0)$ which is the midpoint of RS. From here, it is tempting to ask the following question:

“If the midpoint of PQ is $(0,3)$ and the midpoint of RS is $(3.5,0)$ , is the midpoint of AB, $(3.5,3)$ ?

Figure 3 – A non-horizontal segment AB with midpoint M.

Generalizing the questions above, we might want to ask “If the midpoint the point with coordinates A $(x_1,y_1)$ and B $(x_2, y_2)$ equal to $(\displaystyle\frac {x_1 + x_2}{2}, \displaystyle\frac{y_1 + y_2}{2})$ ?”

If we extend the QA and the horizontal yellow dashed line to the right, we can from two right triangles as shown in Figure 4. From the statements above, we want to show that point M is the midpoint of AB.

To show that M is the midpoint of AB, it is sufficient to show that AM is congruent to MB. This leads us to Figure 5, where we label the right angles of the two triangles T and U. We will now show that triangle AUM is congruent to triangle MTB. If so, then we can show that AM is congruent to MB since they are the corresponding sides of the given triangles.

Proof that AUM is congruent to MTB

Since PB and MT are horizontal segments, we can consider AB as a transversal of parallel segments PB and the segment containing MT. It follows that angle TBM and angle UMA are congruent because they are corresponding angles. It is also clear that BT is congruent to MU, and angle T is congruent to angle U since they are both right angles. Therefore, by the ASA congruence theorem, AUM is congruent to MTB. (For an explanation of parallel lines and transversals, click here).

Since corresponding parts of congruent triangles are congruent, AM is congruent to MB. Hence, M is the midpoint of AB.

Figure 5 – The triangle produced by extending the horizontal lines passing through the three points.

Note that our proof did not talk about coordinates, but the general case. That is, if the coordinates of A are $( x_1, x_2)$ and the coordinates of B are $(y_1, y_2)$ , the coordinates of M is equal to $(\displaystyle\frac{x_1 + x_2}{2},\displaystyle\frac{y_1 +yx_2}{2} )$ .

Delving Deeper

There are also other ways to show that the midpoint of AB is M. $( x_1,y_1)$ and $( x_2,y_2)$ lies on the midpoint formula. The details of the solutions are left to the reader as an exercise.

From Figure 3, draw two right triangles with hypotenuse AM and hypotenuse AB and show that AM is half of AB.
Using the distance formula, show that the distance between point A and point M is the same as the distance between point M and point B.
Show that AM and MB has the same slope.
Get the equation of the line containing AB, and substitute the coordinates of M to the equation of line AB.

3 comments ASA congruence theorem, congruent angles, congruent triangles, congruent triangles geometry, congruent triangles math, coordinate geometry, coordinate geometry midpoint formula, derivation of the midpoint formula, distance formula, geometry parallel lines and transversals, linear measure midpoint formula, midpoint formula, midpoint formula geometry, midpoint line segment formula, side angle side

« 1 … 147 148 149 150 151 … 157 »